题目内容
 (2013•巴中)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
(2013•巴中)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m |
| x |
| 4 |
| 3 |
(1)求反比例函数的解析式;
(2)求△AOB的面积.
分析:(1)过点A作AD⊥x轴,在直角三角形AOD中,根据已知的三角函数值和线段OA的长求出AD与OD的长,得到点A的坐标,代入反比例函数解析式中求出反比例函数的解析式;
(2)把点B的横坐标代入反比例函数解析式中得到B的坐标,然后分别把点A和点B的坐标代入一次函数解析式中,求出k与b的值即可得到一次函数解析式,从而求出点C的坐标,得到OC的长,最后利用三角形的面积公式求出三角形AOC与三角形BOC的面积,相加即可得到三角形AOB的面积.
(2)把点B的横坐标代入反比例函数解析式中得到B的坐标,然后分别把点A和点B的坐标代入一次函数解析式中,求出k与b的值即可得到一次函数解析式,从而求出点C的坐标,得到OC的长,最后利用三角形的面积公式求出三角形AOC与三角形BOC的面积,相加即可得到三角形AOB的面积.
解答: 解:(1)过点A作AD⊥x轴,
解:(1)过点A作AD⊥x轴,
在Rt△AOD中,∵tan∠AOE=
=
,
设AD=4x,OD=3x,
∵OA=5,
在Rt△AOD中,根据勾股定理解得AD=4,OD=3,
∴A(3,4),
把A(3,4)代入反比例函数y=
中,
解得:m=12,
则反比例函数的解析式为y=
;
(2)把点B的坐标为(-6,n)代入y=
中,
解得n=-2,
则B的坐标为(-6,-2),
把A(3,4)和B(-6,-2)分别代入一次函数y=kx+b(k≠0)得
,
解得
,
则一次函数的解析式为y=
x+2,
∵点C在x轴上,令y=0,得x=-3
即OC=3,
∴S△AOB=S△AOC+S△BOC=
×3×4+
×3×2=9.
 解:(1)过点A作AD⊥x轴,
解:(1)过点A作AD⊥x轴,在Rt△AOD中,∵tan∠AOE=
| AD |
| OD |
| 4 |
| 3 |
设AD=4x,OD=3x,
∵OA=5,
在Rt△AOD中,根据勾股定理解得AD=4,OD=3,
∴A(3,4),
把A(3,4)代入反比例函数y=
| m |
| x |
解得:m=12,
则反比例函数的解析式为y=
| 12 |
| x |
(2)把点B的坐标为(-6,n)代入y=
| 12 |
| x |
解得n=-2,
则B的坐标为(-6,-2),
把A(3,4)和B(-6,-2)分别代入一次函数y=kx+b(k≠0)得
|
解得
|
则一次函数的解析式为y=
| 2 |
| 3 |
∵点C在x轴上,令y=0,得x=-3
即OC=3,
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了反比例函数与一次函数的交点问题,勾股定理,三角形函数值,以及三角形的面积公式的运用,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
 (2013•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
(2013•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )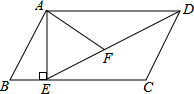 (2013•巴中)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(2013•巴中)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. (2013•巴中)如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
(2013•巴中)如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )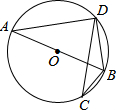 (2013•巴中)如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
(2013•巴中)如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )