Question

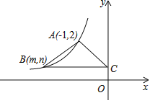
【题目】如图，在平面直角坐标系中，函数(x<0，常数k<0)的图象经过点A(-1，2)，B(m，n)且(m<-1)，过点B作y轴的垂线，垂足为C，若△ABC面积为2，求点B的坐标．

Answer 1

【答案】点的坐标是．

【解析】

由于函数y= （x＜0，常数k＜0）的图象经过点A（-1，2），把（-1，2）代入解析式即可确定k=-2，依题意BC=-m，BC边上的高是2-n=2+，根据三角形的面积公式得到关于m的方程，解方程即可求出m，然后把m的值代入y=- ，即可求得B的纵坐标，最后就求出点B的坐标．

∵ 函数，(x<0,常数k<0)的图象经过点，

∴ 把代入解析式得，

∴ ，

∵ ，

∴ ，当时，，

∴ 边上的高是，

而，

∴ ，

∴ 把代入，

∴ ，

∴ 点的坐标是．