题目内容
下图中表示一次函数y=ax+b与正比例函数y=abx(a,b是常数,且ab≠0)图象是 ( )
A. | B. | C. | D. |
A
解析试题分析:A.正比例函数y=abx过第二、四象限,所以a<0,b>0,而y=ax+b过第一、二、四象限,所以a<0,b>0,故A正确;B.正比例函数y=abx过第一、三象限,所以a>0,b<0,而y=ax+b过第一、二、四象限,所以a<0,b>0,所以矛盾,故B错误;C.正比例函数y=abx过第二、四象限,所以a<0,b>0,而y=ax+b过第一、二、三象限,所以a>0,b>0,所以矛盾,故C错误;D.正比例函数y=abx过第一、三象限,所以a>0,b<0,而y=ax+b过第一、三、四象限,所以a<0,<0,所以矛盾,故D错误,故选:A.
考点:一次函数的图象性质.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
方程 ,则
,则 等于()
等于()
| A.15 | B.16 | C.17 | D.34 |
 与
与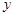 的值相等,则已知程方组
的值相等,则已知程方组 中
中 的值是( ).
的值是( ).
| A.1 | B. | C. | D. |
(本题满分8分)九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是
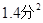 ,则成绩较为整齐的是 队.
,则成绩较为整齐的是 队. 
 是y关于x的一次函数,则m=______.
是y关于x的一次函数,则m=______. 的图象经过点A(?3,?2).
的图象经过点A(?3,?2).