题目内容
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在符合条件的点
;(3)存在符合条件的点![]() 共有4个,分别为
共有4个,分别为 ![]()
![]()
![]()
![]()
【解析】
(1)利用三角函数求得OA以及OC的长度,则B的坐标即可得到;
(2)分别求出D点和E点坐标,即可求得DE的解析式;
(3)分当FM是菱形的边和当OF是对角线两种情况进行讨论.利用三角函数即可求得N的坐标.
(1)在直角△OAC中,tan∠ACO=![]() ,
,
∴设OA=![]() x,则OC=3x,
x,则OC=3x,
根据勾股定理得:(3x)2+(![]() x)2=AC2,
x)2=AC2,
即9x2+3x2=576,
解得:x=4![]() .
.
则C的坐标是:(12![]() ,0),B的坐标是(
,0),B的坐标是(![]() );
);
(2)由折叠可知![]()
![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ∥
∥![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,则
,则![]() ,
,
解得![]() ;
;
∴![]() .
.
(3)∵OF为Rt△AOC斜边上的中线,
∴OF=![]() AC=12,
AC=12,
∵![]()
![]() ,
,
∴tan∠EDC=![]()
∴DE与x轴夹角是60°,
当FM是菱形的边时(如图1),ON∥FM,
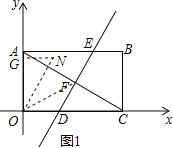
∴∠NOC=60°或120°.
当∠NOC=60°时,过N作NG⊥y轴,
∴NG=ONsin30°=12×![]() =6,OG=ONcos30°=12×
=6,OG=ONcos30°=12×![]() =6
=6![]() ,
,
此时N的坐标是(6,6![]() );
);
当∠NOC=120°时,与当∠NOC=60°时关于原点对称,则坐标是(-6,-6![]() );
);
当OF是对角线时(如图2),MN关于OF对称,
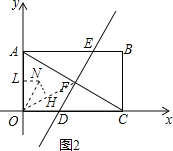
∵F的坐标是(6![]() ,6),
,6),
∴∠FOD=∠NOF=30°,
在直角△ONH中,OH=![]() OF=6,ON=
OF=6,ON=![]() .
.
作NL⊥y轴于点L.
在直角△ONL中,∠NOL=30°,
∴NL=![]() ON=
ON=![]() ,OL=ONcos30°=
,OL=ONcos30°=![]() ×
×![]() =6.
=6.
此时N的坐标是(/span>![]() ,6).
,6).
当DE与y轴的交点时M,这个时候N在第四象限,
此时点N的坐标为:(6![]() ,-6).
,-6).
则N的坐标是:(6![]() ,-6)或(6,6
,-6)或(6,6![]() )或(-6,-6
)或(-6,-6![]() )或(2
)或(2![]() ,6).
,6).