Question

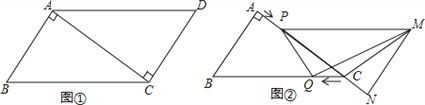
【题目】已知，如图①，在ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：

（1）当t为何值时，PQ∥MN？

（2）设△QMC的面积为y（cm2），求y与t之间的函数关系式；

（3）是否存在某一时刻t，使S△QMC：S四边形ABQP=1：4？若存在，求出t的值；若不存在，请说明理由．

（4）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】t=；y=－；1:4；t=

【解析】试题分析： 当PQ∥MN时，可得： ，从而得到： ，解方程求出的值；

作于点，则可以得到，根据相似三角形的性质可以求出， ，利用三角形的面积公式求出与的关系式；

根据S△QMC: 可以得到关于的方程，解方程求出的值；

作于点， 于点，则△CPD∽△CBA，利用相似三角形的性质可以得到： ，解方程求出的值.

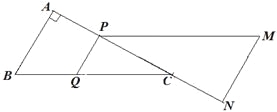
试题解析：(1)如图所示，

若PQ∥MN，则有，

∵， ， ，

∴，

即，

解得.

(2)如图所示，

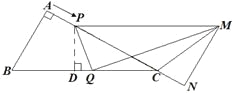
作于点，则△CPD∽△CBA，

∴,

∵， ， ，

∴，

∴

又∵，

∴△QMC的面积为：

(3)存在时，使得S△QMC: .

理由如下：

∵PM∥BC

∴

∵S△QMC: ，

∴S△PQC: S△ABC=1:5，

∵

.∴

∴

∴

∴存在当时，S△QMC: ；

(4)存在某一时刻，使.

理由如下：

如图所示，

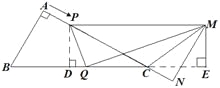
作于点， 于点，则△CPD∽△CBA，

∴,

∵， ， ， ，

∴，

∴， .

∵PQ⊥MQ，

∴△PDQ∽△QEM，

∴，

即

∵，

，

，

∴，

即，

∴， （舍去）

∴当时，使PQ⊥MQ.