题目内容
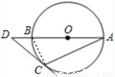
AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠BAC=25°,则∠ADC等于( )
A.20° B.30° C.40° D.50°
【答案】
C.
【解析】
试题分析:先连接BC,由于AB是直径,可知∠BCA=90°,而∠BAC=25°,易求∠CBA,又DC是切线,利用弦切角定理可知∠DCB=∠BAC=25°,再利用三角形外角性质可求∠ADC.
如图所示,连接BC,
∵AB是直径,
∴∠BCA=90°,
又∵∠BAC=25°,
∴∠CBA=90°-25°=65°,
∵DC是切线,
∴∠BCD=∠A=25°,
∴∠ADC=∠CBA-∠BCD=65°-25°=40°.
故选C.
考点:1.切线的性质;2.圆周角定理.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,点D是
如图,AB是⊙O的直径,点D是
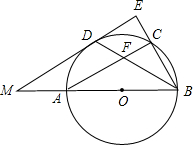
 已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.
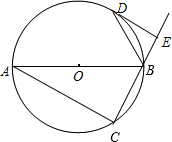
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E. (2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.
(2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.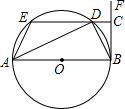 如图,AB是⊙O的直径,点C在⊙O的切线BF上,过C作直线CE⊥BF,交⊙O于点D、点E,连接AE、
如图,AB是⊙O的直径,点C在⊙O的切线BF上,过C作直线CE⊥BF,交⊙O于点D、点E,连接AE、