��Ŀ����
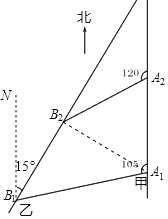
����Ŀ����ͼ���״���ÿСʱ30![]() ������ٶ������������У����״�λ��A1��ʱ���Ҵ�λ�ڼ״��ı�ƫ��105�������B1�������Ҵ���B1������ƫ��15����������ֱ�ߺ��У����״�����20���ӵ���A2ʱ���Ҵ����е��״��ı�ƫ��120�������B2������ʱ�������10
������ٶ������������У����״�λ��A1��ʱ���Ҵ�λ�ڼ״��ı�ƫ��105�������B1�������Ҵ���B1������ƫ��15����������ֱ�ߺ��У����״�����20���ӵ���A2ʱ���Ҵ����е��״��ı�ƫ��120�������B2������ʱ�������10![]() ���
���
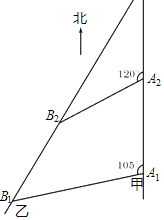
��1���жϡ�A1A2B2����״��������֤����
��2�����Ҵ�ÿСʱ���ж��ٺ��
���𰸡���1����A1A2B2�ǵȱ������Σ���2��20![]() ����
����
��������
��1���ɸ����ĽǶȼ������θ��߳����ó���A1A2B2����״.
��2�������B1B2�ľ���������ʱ������Ҵ����е��ٶ�.
��1����A1A2B2�ǵȱ������Σ��������£�
����A1B2��
�״���ÿСʱ30![]() ������ٶ������������У�����20���ӵ���A2��
������ٶ������������У�����20���ӵ���A2��
��A1A2��30![]() ��10
��10![]() ��
��
�֡�A2B2��10![]() ����A1A2B2��60����
����A1A2B2��60����
���A1A2B2�ǵȱ������Σ�
��2������B��B1N��A1A2����ͼ��
��B1N��A1A2��
���A1B1N��180������B1A1A2��180����105����75����
���A1B1B2��75����15����60����
�ߡ�A1A2B2�ǵȱ������Σ�
���A2A1B2��60����A1B2��A1A2��10![]() ��
��
���B1A1B2��105����60����45����
�ڡ�B1A1B2�У�
��A1B2��10![]() ����B1A1B2��45������A1B1B2��60����
����B1A1B2��45������A1B1B2��60����
����B��BE��A1B1,
�����Ҷ��������B1B2�� ��
��
�����Ҵ�ÿСʱ���У�![]() ���
���