题目内容
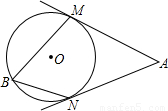
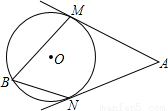
如图，AM、AN分别切⊙O于M、N两点，点B在⊙O上，且∠MBN=70°，则∠A= 度．
【答案】分析：连接OM，ON，AM、AN分别切⊙O于M、N两点，则∠OMA=∠ONA=90°；由圆周角定理知，∠MON=2∠B=140°，所以利用四边形内角和可求得∠A=40°．
解答：
解：连接OM，ON，则∠OMA=∠ONA=90°，
∵∠MON=2∠B=140°，
∴∠A=360°-90°-90°-∠MON=40°．
点评：本题利用了切线的概念，四边形的内角和为360度，圆周角定理求解．
解答：
解：连接OM，ON，则∠OMA=∠ONA=90°，∵∠MON=2∠B=140°，
∴∠A=360°-90°-90°-∠MON=40°．
点评：本题利用了切线的概念，四边形的内角和为360度，圆周角定理求解．
练习册系列答案
相关题目
16、如图，AM、AN分别切⊙O于M、N两点，点B在⊙O上，且∠MBN=70°，则∠A=
