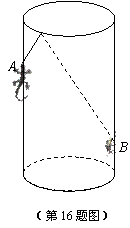题目内容
 如图,圆柱形容器中,高为1.2m,底面周长为1.6m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
如图,圆柱形容器中,高为1.2m,底面周长为1.6m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为| 2 |
| 5 |
| 13 |
| 2 |
| 5 |
| 13 |
分析:将容器侧面展开,建立A关于EC的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解答:解:如图:

∵高为1.2m,底面周长为1.6m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.8m,BD=1.2m,
∴将容器侧面展开,作A关于EC的对称点A′,
连接A′B交EC于F,则A′B即为最短距离,
A′B=
=
=
(m).
故答案为:
.

∵高为1.2m,底面周长为1.6m,在容器内壁离容器底部0.3m的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,
∴A′D=0.8m,BD=1.2m,
∴将容器侧面展开,作A关于EC的对称点A′,
连接A′B交EC于F,则A′B即为最短距离,
A′B=
| A′D2+BD2 |
| 0.82+1.22 |
| 2 |
| 5 |
| 13 |
故答案为:
| 2 |
| 5 |
| 13 |
点评:本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目