题目内容
 如图,⊙O的弦AB垂直平分半径OC,垂足为D,若CD=
如图,⊙O的弦AB垂直平分半径OC,垂足为D,若CD= ,则AB的长为
,则AB的长为
- A.

- B.

- C.

- D.

D
分析:连接OC,由题意即可推出OC的长度可得OA的长度,运用勾股定理即可推出AD的长度,然后,通过垂径定理即可推出AB的长度.
解答: 解:连接OA,
解:连接OA,
∵⊙O的弦AB垂直平分半径OC,CD= ,
,
∴OC= ,
,
∴OA= ,
,
∵OC⊥AB,
∴AD= ,
,
∵AB=2AD,
∴AD= .
.
故选D.
点评:本题主要考查垂径定理、勾股定理的应用,关键在于正确地作出辅助线构建直角三角形,认真地进行计算.
分析:连接OC,由题意即可推出OC的长度可得OA的长度,运用勾股定理即可推出AD的长度,然后,通过垂径定理即可推出AB的长度.
解答:
 解:连接OA,
解:连接OA,∵⊙O的弦AB垂直平分半径OC,CD=
 ,
,∴OC=
 ,
,∴OA=
 ,
,∵OC⊥AB,
∴AD=
 ,
,∵AB=2AD,
∴AD=
 .
.故选D.
点评:本题主要考查垂径定理、勾股定理的应用,关键在于正确地作出辅助线构建直角三角形,认真地进行计算.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目

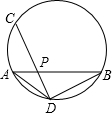





 ,即可得到OC,AB
,即可得到OC,AB
 OP,则OP=
OP,则OP=