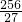题目内容
周长相同的正三角形、正方形、正六边形的面积分别为S1、S2、S3，则其三者的大小关系为：________．
S3＞S2＞S1
分析：不妨设周长为12a，则正三角形边长为4a，正方形边长为3a，正六边形边长为2a，即可求得三个正多边形的面积，即可进行比较．
解答：不妨设周长为12a，则正三角形边长为4a，正方形边长为3a，正六边形边长为2a．
所以：S1=4
a2 S2=9a 2 S3=6a 2
比较可得S3＞S2＞S1．
故答案是：S3＞S2＞S1．
点评：本题主要考查了正多边形的计算，正确设未知数是解题的关键．
分析：不妨设周长为12a，则正三角形边长为4a，正方形边长为3a，正六边形边长为2a，即可求得三个正多边形的面积，即可进行比较．
解答：不妨设周长为12a，则正三角形边长为4a，正方形边长为3a，正六边形边长为2a．
所以：S1=4
a2 S2=9a 2 S3=6a 2比较可得S3＞S2＞S1．
故答案是：S3＞S2＞S1．
点评：本题主要考查了正多边形的计算，正确设未知数是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
