题目内容
如图，Rt△ABC，∠C=90°，AD平分∠CAB，DE⊥AB于E，则下列结论中不正确的是
- A.BD+ED=BC
- B.DE平分∠ADB
- C.AD平分∠EDC
- D.ED+AC＞AD
B
分析：根据已知条件由角平分线的性质可得结论CD=DE，由此又可得出很多结论，对各选项逐个验证，证明．
解答：CD=DE，
∴BD+DE=BD+CD=BC；
又有AD=AD，
可证△AED≌△ACD
∴∠ADE=∠ADC
即DE平分∠ADB；
在△ACD中，CD+AC＞AD
所以ED+AC＞AD．
故选B．
点评：本题主要考查平分线的性质，由已知证明△AED≌△ACD是解决的关键．
分析：根据已知条件由角平分线的性质可得结论CD=DE，由此又可得出很多结论，对各选项逐个验证，证明．
解答：CD=DE，
∴BD+DE=BD+CD=BC；
又有AD=AD，
可证△AED≌△ACD
∴∠ADE=∠ADC
即DE平分∠ADB；
在△ACD中，CD+AC＞AD
所以ED+AC＞AD．
故选B．
点评：本题主要考查平分线的性质，由已知证明△AED≌△ACD是解决的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，Rt△ABC中，∠C=90°，BC=6cm，AC=8cm，点P从B点出发，以2cm/s的速度向点C运动，点Q从C点出发，以1cm/s的速度向点A运动．若P，Q同时出发，则经过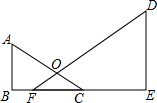
已知，如图，Rt△ABC中∠B=90°，Rt△DEF中∠E=90°，OF=OC，AB=6，BF=2，CE=8，CA=0，DE=15．
（2013•封开县一模）如图，Rt△ABC的直角边BC=8，AC=6