题目内容
【题目】已知，抛物线y=ax2+bx+4 与x轴交于点A（﹣3，0）和B（2，0），与y轴交于点C．
（1）求抛物线的解析式；
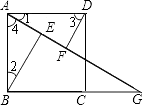
（2）如图1，若点D为CB的中点，将线段DB绕点D旋转，点B的对应点为点G，当点G恰好落在抛物线的对称轴上时，求点G的坐标；
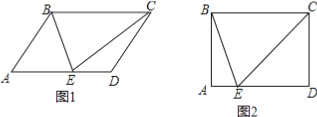
（3）如图2，若点D为直线BC或直线AC上的一点，E为x轴上一动点，抛物线
y=ax2+bx+4对称轴上是否存在点F，使以B，D，F，E为顶点的四边形为菱形？若存在，请求出点F的坐标；若不存在，请说明理由．
【答案】
（1）解：∵抛物线y=ax2+bx+4 与x轴交于点A（﹣3，0）和B（2，0），
∴ 
，解得 
，
∴抛物线解析式为y=﹣ 
x2﹣ x+4
（2）解：由（1）可知抛物线的对称轴为x=﹣ 
．
∴可设点G的坐标为（﹣ ，y），
∵点D是BC的中点，
∴点D的坐标为（1，2），
在Rt△OBC中，BC= 
=2 
．
∴DB= BC= ，
由旋转的性质可知，DG=DB，
∴（﹣ ﹣1）2+（y﹣2）2=5，解得：y=2+ 
或y=2﹣ ，
∴点G的坐标为（﹣ ，2+ ）或（﹣ ，2﹣ ）
（3）解：①当BE为对角线时，因为菱形的对角线互相垂直平分，所以此时D即为对称轴与AC的交点，F为点D关于x轴的对称点，
设直线AC解析式为y=kx+b，
∵C（0，4），A（﹣3，0）
∴ 
，解得 
，
∴直线AC解析式为y= 
x+4，
∴当 
时， 
，
∴D 
，
∴F 
；
②当BE为菱形的边时，有DF∥BE
I）当点D在直线BC上时，可求得直线BC解析式为y=﹣2x+4，
设D（a，﹣2a+4），则点F 
，
∵四边形BDFE是菱形，
∴FD=DB，
∴ 
，解得 
， 
，
∴F 
或 
；
II）当点D在直线AC上时，
设D 
，则点F 
，
∵四边形BFDE是菱形，
∴FD=FB，
∴（a+ ）2=（2+ ）2+（ a+4）2，解得：a1=﹣3（舍去）， 
，
∴F 
，
综上所述，点F的坐标分别为 或 或 或
【解析】（1）把A、B两点的坐标代入抛物线解析式可求得a、b的值，可求得抛物线解析式；（2）可设出G点坐标，利用旋转的性质可求得DG=DB，从而可列出方程，可求得G点坐标；（3）分BE为对角线和BE为边两种情况，①当BE为对角线时，则可知BE⊥DF，可知D为对称轴与直线AC的交点，F为D点关于x轴的对称点，可先求得直线AC的解析式，可求得D点坐标，则容易求得F点坐标；②当BE为边时，可利用直线BC或直线AC的解析式设出点D的坐标，从而可表示出F点的坐标，再利用菱形的性质可列出方程，从而可求得F点的坐标．
