题目内容
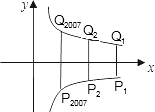 如图:已知反比例函数y=
如图:已知反比例函数y=| 6 |
| x |
| 2 |
| x |
| 6 |
| x |
| 2 |
| x |
分析:先根据反比例函数y=
当x>0时Q1(x1,2),Q2(x2,4),Q3(x3,6)…Q2007找出规律,得出x=2007时y的值,设P1、P2、P3三点的坐标分别为P1(x1,y1)、P2(x2,y2)、P3(x3,y3)分别把Q1(x1,2),Q2(x2,4),Q3(x3,6)三点的坐标代入函数y=
,分别求出x1,x2,x3的值,再把此三点的横坐标代入反比例函数y=-
中求出P1、P2、P3三点的纵坐标,找出Q1、Q2、Q3的纵坐标与P1、P2、P3三点的纵坐标的关系即可解答.
| 6 |
| x |
| 6 |
| x |
| 2 |
| x |
解答:解:∵Q1(x1,2),Q2(x2,4),Q3(x3,6)三点中,2=1×2,4=2×2,6=3×2…,
∴当Q2007的纵坐标为2007×2=4014,
分别把Q1(x1,2),Q2(x2,4),Q3(x3,6)三点的坐标代入函数y=
得,
2=
,4=
,6=
,
解得,x1=3,x2=
,x3=1,
把x1,x2,x3的值代入y=-
得,y1=-
,y2=-
,y3=-2,
故P1、P2、P3三点的坐标分别为P1(x1,-
)、P2(x2,-
)、P3(x3,-2),
∵-
=2÷(-3),-
=4÷(-3),-2=6÷(-3),
∴P2007的纵坐标为Q2007的纵坐标除以-3,即4014÷(-3)=-1338.
∴当Q2007的纵坐标为2007×2=4014,
分别把Q1(x1,2),Q2(x2,4),Q3(x3,6)三点的坐标代入函数y=
| 6 |
| x |
2=
| 6 |
| x1 |
| 6 |
| x2 |
| 6 |
| x3 |
解得,x1=3,x2=
| 3 |
| 2 |
把x1,x2,x3的值代入y=-
| 2 |
| x |
| 2 |
| 3 |
| 4 |
| 3 |
故P1、P2、P3三点的坐标分别为P1(x1,-
| 2 |
| 3 |
| 4 |
| 3 |
∵-
| 2 |
| 3 |
| 4 |
| 3 |
∴P2007的纵坐标为Q2007的纵坐标除以-3,即4014÷(-3)=-1338.
点评:本题考查的是反比例函数图象上点的坐标特点,由两函数的图象找出Q1、Q2、Q3及P1、P2、P3三点横纵坐标之间的关系是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=