题目内容
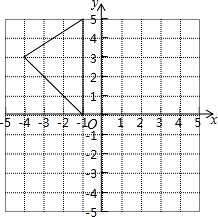
如图,平面内有公共端点的 6 条射线 OA,OB,OC,OD,OE,OF,依照图中的规律,从射线 OA 开始,按逆时针方向,一次在射线上画点表示 1,2,3,4,5,6,7,…
(1)根据图中规律,表示“19”的点在射线 上; 按照图中规律推算,表示“2016”的点在射线 上;
(3)请你写出在射线 OC 上表示的数的规律(用含 n 的代数式表示) .

【考点】规律型:数字的变化类;规律型:图形的变化类.
【分析】(1)根据观察,可发现规律:OA 上的点是 6n﹣5,OB 上的点是 6n﹣4,CO 上的点是 6n
﹣3,OD 上的点是 6n﹣2,OE 上的点是 6n﹣1,OF 上的点是 6n,19 是 24 减 5,可得答案; 根据观察,可发现规律:OA 上的点是 6n﹣5,OB 上的点是 6n﹣4,CO 上的点是 6n﹣3,OD 上的 点是 6n﹣2,OE 上的点是 6n﹣1,OF 上的点是 6n,2016 是 6 的倍数,可得答案;
(3)根据观察,可发现规律:OA 上的点是 6n﹣5,OB 上的点是 6n﹣4,CO 上的点是 6n﹣3,OD
上的点是 6n﹣2,OE 上的点是 6n﹣1,OF 上的点是 6n,可得答案.
【解答】解:(1)根据图中规律,表示“19”的点在射线 OA 上; 按照图中规律推算,表示“2016”的点在射线 DF 上;
(3)在射线 OC 上表示的数的规律(用含 n 的代数式表示) 6n﹣3. 故答案为:OA,DF,6n﹣3.
【点评】本题考查了数字的变化类,观察数据发现规律:OA 上的点是 6n﹣5,OB 上的点是 6n﹣4, CO 上的点是 6n﹣3,OD 上的点是 6n﹣2,OE 上的点是 6n﹣1,OF 上的点是 6n 是解题关键.

 y﹣1 是( )
y﹣1 是( )
 A.
A.  B.
B. C.
C.  D.
D.