题目内容
已知直线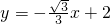 与y轴交于点A,与x轴交于点B;若点P是直线AB上的一动点,坐标平面中存在点Q,使以O、B、P、Q为顶点的四边形为菱形,则点Q的坐标是________.
与y轴交于点A,与x轴交于点B;若点P是直线AB上的一动点,坐标平面中存在点Q,使以O、B、P、Q为顶点的四边形为菱形,则点Q的坐标是________.
( ,-1),(-3,
,-1),(-3, ),(3,-
),(3,- ),(
),( ,3)
,3)
分析:本题需先根据已知条件画出图形,再根据图形求出相应线段的长度即可求出点Q的坐标.
解答:(1)如图

过点Q做QC⊥OB
∵OB=2
∴OC=
∴QC=tan30°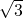 =1
=1
∴点Q的坐标是(
(2)

过点Q做QC⊥OB
∵OB=2
∴
∴CQ=
∴OC=-3
∴Q的坐标是(-3, )
)
(3)如图

连△OQB是等边三角形
∵OB=2
∴ QC=3
QC=3
∴Q的坐标是( ,3)
,3)
(4)

过点Q做QC⊥OB
∵OB=
∴
∴ =
=
∴OC=3
∴Q的坐标是(3,- )
)
故答案为( ,(3,-
,(3,- ),(
),( ,3)(3,-
,3)(3,- )
)
点评:本题主要考查了一次函数的综合题,本题中根据P是直线AB上的一动点求出各点的坐标是解题的关键,这是一道常考题型.
 ,-1),(-3,
,-1),(-3, ),(3,-
),(3,- ),(
),( ,3)
,3)分析:本题需先根据已知条件画出图形,再根据图形求出相应线段的长度即可求出点Q的坐标.
解答:(1)如图

过点Q做QC⊥OB
∵OB=2

∴OC=

∴QC=tan30°
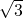 =1
=1∴点Q的坐标是(

(2)

过点Q做QC⊥OB
∵OB=2

∴

∴CQ=

∴OC=-3
∴Q的坐标是(-3,
 )
)(3)如图

连△OQB是等边三角形
∵OB=2

∴
 QC=3
QC=3∴Q的坐标是(
 ,3)
,3)(4)

过点Q做QC⊥OB
∵OB=

∴

∴
 =
=
∴OC=3
∴Q的坐标是(3,-
 )
)故答案为(
 ,(3,-
,(3,- ),(
),( ,3)(3,-
,3)(3,- )
)点评:本题主要考查了一次函数的综合题,本题中根据P是直线AB上的一动点求出各点的坐标是解题的关键,这是一道常考题型.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 已知直线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=
已知直线与y轴交于点B(0,1),与抛物线交于x轴上一点A,且tan∠BAO=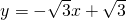 与x轴交于点A,与y轴交于点B,C是x轴上一点,如果∠ABC=∠ACB,
与x轴交于点A,与y轴交于点B,C是x轴上一点,如果∠ABC=∠ACB, 与y轴交于点A,抛物线
与y轴交于点A,抛物线 经过点A,其顶点为B,另一抛物线
经过点A,其顶点为B,另一抛物线 的顶点为D,两抛物线相交于点C
的顶点为D,两抛物线相交于点C
 的理由;
的理由;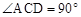 ,求m的值
,求m的值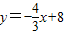 与x轴交于点A,与y轴交于点B,C是线段AB的中点.抛物线y=ax2+bx+c(a>0)过O、A两点,且其顶点的纵坐标为
与x轴交于点A,与y轴交于点B,C是线段AB的中点.抛物线y=ax2+bx+c(a>0)过O、A两点,且其顶点的纵坐标为 .
.