题目内容
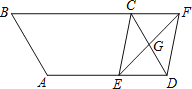
【题目】如图所示，D是等边三角形ABC外一点，
，点E，F分别在
上
（1）求证：AD是BC的垂直平分线
（2）若ED平分
，求证FD平分
．
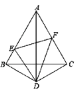
【答案】（1）见解析；（2）见解析
【解析】
（1）求出AB=AC，BD=DC，根据线段垂直平分线性质求出即可；（2）过D作DM⊥EF，连接AD，求出AD平分∠BAC，求出∠ABC=∠ACB=60°，求出BD=DM，BD=DC，推出DM=DC即可.
（1）证明：
是等边三角形，
∴A在的BC垂直平分线上，
，
∴D在BC的垂直平分线上，
∴AD是BC的垂直平分线上；
（2）如图，过D作
，连接AD，
是BC的垂直平分线，
∴AD平分
，
是等边三角形，
，
，
∴∠DBC=∠DCB=30°，
∴∠ABD=∠ACD=90°，
，
平分
，AD平分，
，
，
∴
平分
．
练习册系列答案
走进文言文系列答案
相关题目
【题目】已知二次函数y=ax2-4x+c，函数值y与自变量x之间的部分对应值如表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
（1）求这个二次函数的关系式．
（2）直接写出m、n、k之间的大小关系．（用“＞”连接）
（3）若点P在这个二次函数的图象上，且点P到x轴的距离为1，求点P的坐标．
