题目内容

如图，以的直角边为直径的半圆，与斜边交于，是边上的中点. 连结,. 试问与半圆相切吗？若相切，请给出证明；若不相切，请说明理由.
解：（1）DE与半圆O相切.               
证明： 连结OD                           
∵AB是半圆O的直径
∴∠BDA=∠BDC=90°                         
∵在Rt△BDC中,E是BC边上的中点
∴DE="BE                                    "
∴∠EBD＝∠BDE                              
∵OB=OD∴∠OBD=∠ODB                             
又∵∠ABC＝∠OBD+∠EBD＝90°
∴∠ODB+∠EDB=90°                          
∴DE与半圆O相切.解析:
p;【解析】略
练习册系列答案
相关题目
19、如图所示，在直角坐标系中，矩形OBCD的边长OB=4，OD=2．
（1）P是OB上一个动点，动点Q在PB或其延长线上运动，OP=PQ，作以PQ为一边的正方形PQRS，点P从O点开始沿线段OB方向运动，直到点P与点B重合，设OP=x，正方形PQRS与矩形OBCD重叠部分的面积为y，写出y与x的函数关系式；
（2）在（1）中，当x分别取1和3时，y的值分别是多少？
（3）已知直线l：y=ax-a经过一定点A，求经过定点A且把矩形OBCD的面积平均分成两部分的直线l的函数解析式．
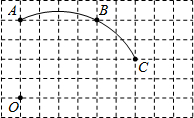精英家教网如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；
②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C
 
；D（
 
）；
②⊙D的半径=
 
（结果保留根号）；
③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面的面积为
 
；（结果保留π）
④若E（7，0），试判断直线EC与⊙D的位置关系，并说明你的理由．
如图，平面直角坐标系中，矩形ABCO的边OA在y正半轴上，OC在x正半轴上，点D是线段OC上一点，过点D作DE⊥AD交直线BC于点E，以A、D、E为顶点作矩形ADEF．
（1）求证：△AOD∽△DCE；
（2）若点A坐标为（0，4），点C坐标为（7，0）．
①当点D的坐标为（5，0）时，抛物线y=ax2+bx+c过A、F、B三点，求点F的坐标及a、b、c的值；
②若点D（k，0）是线段OC上任意一点，点F是否还在①中所求的抛物线上？如果在，请说明理由；如果不在，请举反例说明；
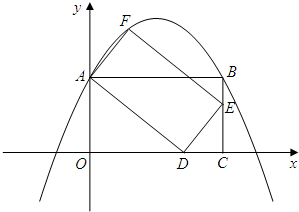（3）若点A的坐标是（0，m），点C的坐标是（n，0），当点D在线段OC上运动时，是否也存在一条抛物线，使得点F都落在该抛物线上？若存在，请直接用含m精英家教网、n的代数式表示该抛物线；若不存在，请说明理由．
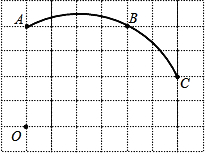精英家教网如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：A
 
、B
 
、C
 
、D
 
；
②⊙D的半径=
 
（结果保留根号）；
③求∠ADC的度数（写出解答过程）
④若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面的半径．
精英家教网如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长，建立平面直角坐标系；②用直尺和圆规画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．
（2）请在（1）的基础上，完成下列问题：
①写出点的坐标：C
 
、D
 
；
②⊙D的半径=
 
（结果保留根号）；
③若扇形ADC是一个圆锥的侧面展开图，则该圆锥的底面面积为
 
（结果保留π）；
④若E（7，0），试判断直线EC与⊙D的位置关系并说明你的理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网