题目内容
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC=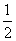 ,求⊙O的半径.
,求⊙O的半径.
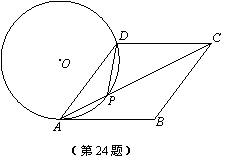
(1)直线AB与⊙O相切.
连结OA、OP,设OP与AD交于点H.
∵PA=PD,∴P为 的中点
的中点
 ∴OP⊥AD,∴∠AHP=90°
∴OP⊥AD,∴∠AHP=90°
∵四边形ABCD是菱形,∴∠DAC=∠BAC,
又∵OA=OP,∴∠OAP=∠OPA.……2分
∵在Rt△AHP中,∠DAP+∠OPA=90°.
∴∠OAB=∠OAP+∠BAC=∠OPA+∠DAP=90°.
 即OA⊥AB,
即OA⊥AB,
∵点A在⊙O上,∴直线AB与⊙O相切.
(2)连结BD交AC于点E,则AC⊥BD.设⊙O的半径为r.
∵在Rt△AED中,AC=8,tan∠DAC=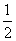 ,∴DE=2
,∴DE=2
由勾股定理,得AD= =
= =2
=2 ,∴AH=
,∴AH= .
.
在Rt△AHP中,由 ,tan∠DAC=
,tan∠DAC=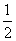 ,得HP=
,得HP=
在Rt△AHO中,由勾股定理得:AH2+OH2=OA2,即( )2+(r-
)2+(r-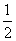
 )2=r 2,
)2=r 2,
解得:r=
 .
.

以下是根据南京市国民经济和社会发展统计公报中的相关数据,绘制统计图的
 一部分.
一部分.
请根据以上信息解答下列问题:
(1)2012年南京市私人轿车拥有是多少万辆?
(2)补全条形统计图;
(3)经测定,汽车的碳排放量与汽车的排量大小有关.如驾驶排量1.6L的轿车,
若一年行驶里程1万千米,则这一年,该轿车的碳排放量约为2.7吨.
经调查,南京市某小区的300辆私人轿车,不同排量的数量统计如下表:
| 排量(L) | 小于1.6 | 1.6 | 1.8 | 大于1.8 |
| 数量(辆) | 30 | 150 | 62 | 58 |
请按照上述的统计数据,通过计算估计,2013年南京市仅排量为1.6L的私人轿车
(假定每辆车平均一年行驶的路程都为1万千米)的碳排放总量约为多少万吨?
计算2×(-9)-18×( -
- )的结果是
)的结果是
| A.-24 | B.-12 | C.-9 | D.6 |
问题提出
平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一
直线上),能否在同一个圆呢?
初步思考
设不在同一条直线上的三点A、B、C确定的圆为⊙O.
⑴当C、D在线段AB的同侧时,
如图①,若点D在⊙O上,此时有∠ACB=∠ADB,理由是 ;
如图②,若点D在⊙O内,此时有∠ACB ∠ADB;
如图③,若点D在⊙O外,此时有∠ACB ∠ADB.(填“=”、“>”或“<”);

由上面的探究,请直接写出A、B、C、D四点在同一个圆上的条件: .
类比学习
(2)仿照上面的探究思路,请探究:当C、D在线段AB的异侧时的情形.
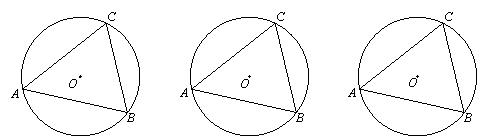 |
此时有 , 此时有 , 此时有 .
由上面的探究,请用文字语言直接写出A、B、C、D四点在同一个圆上的条件: .
拓展延伸
 (3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图,AB是⊙O的直径,点C在⊙O上.
求作:CN⊥AB.
作法:①连接CA, CB;
CB;
②在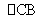 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M;
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图④中作图,并说明CN⊥AB的理由.(提示:可以利用(2)中的结论)
 -
- ×
× = .
= .

 有意义的x的取值范围是 .
有意义的x的取值范围是 . 的最简公分母是 .
的最简公分母是 .