题目内容
 如图,OA、OB、OC是⊙O的三条半径,M、N分别是OA、OB上两点,且AM=20M,BN=20N,MC=NC,求证:
如图,OA、OB、OC是⊙O的三条半径,M、N分别是OA、OB上两点,且AM=20M,BN=20N,MC=NC,求证: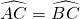 .
.
证明:∵OA=OB,AM=20M,BN=20N,
∴OM=ON,
在△OCM和△OCN中,
 ,
,
∴△OCM≌△OCN(SSS),
∴∠AOC=∠BOC,
∴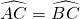 .
.
分析:由AM=20M,BN=20N,易得OM=ON,又由MC=NC,易证得△OMC≌ONC,则可得∠AOC=∠BOC,又由圆心角与弧的关系,即可证得结论.
点评:此题考查了圆心角与弧的关系以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
∴OM=ON,
在△OCM和△OCN中,
 ,
,∴△OCM≌△OCN(SSS),
∴∠AOC=∠BOC,
∴
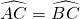 .
.分析:由AM=20M,BN=20N,易得OM=ON,又由MC=NC,易证得△OMC≌ONC,则可得∠AOC=∠BOC,又由圆心角与弧的关系,即可证得结论.
点评:此题考查了圆心角与弧的关系以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 40、已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC.
40、已知:如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点.求证:MC=NC.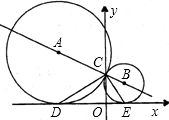 已知:如图,OA与oB外切于点C,DE是两圆的一条外公切线,切点分别为D、E.
已知:如图,OA与oB外切于点C,DE是两圆的一条外公切线,切点分别为D、E. 如图,OA、OB是⊙O的半径,OA⊥OB,C为OB延长线上一点,CD切⊙O于点D,E为AD与OC的交点,连接OD.已知CE=5,求线段CD的长.
如图,OA、OB是⊙O的半径,OA⊥OB,C为OB延长线上一点,CD切⊙O于点D,E为AD与OC的交点,连接OD.已知CE=5,求线段CD的长. 如图,OA,OB,OC,OD,OE是平面内有公共端点的五条射线,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…在射线OE上数字的排列规律为5n,射线OC上数字的排列规律为5n-2(n≥1的正整数)
如图,OA,OB,OC,OD,OE是平面内有公共端点的五条射线,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…在射线OE上数字的排列规律为5n,射线OC上数字的排列规律为5n-2(n≥1的正整数) 如图,OA,OB是两条公路,C,D是两所大学,求作一点P,使它到OA,OB的距离和到C,D的距离相等.保留作图痕迹.
如图,OA,OB是两条公路,C,D是两所大学,求作一点P,使它到OA,OB的距离和到C,D的距离相等.保留作图痕迹.