Question

用反证法证明：两条直线被第三条直线所截．如果同旁内角不互补，那么这两条直线不平行．
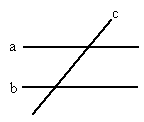
已知：如图，直线l₁，l₂被l₃所截，∠1+∠2≠180°．
求证：l₁与l₂不平行．
证明：假设l₁________l₂，
则∠1+∠2________180°（两直线平行，同旁内角互补）
这与________矛盾，故________不成立．
所以________．

Answer 1

∥    =    ∠1+∠2≠180°    假设    l₁与l₂不平行
分析：用反证法证明问题，先假设结论不成立，即l₁∥l₂，根据平行线的性质，可得∠1+∠2=180°，与已知相矛盾，从而证得l₁与l₂不平行．
解答：证明：假设l₁∥l₂，
则∠1+∠2=180°（两直线平行，同旁内角互补），
这与∠1+∠2≠180°矛盾，故假设_不成立．
所以结论成立，l₁与l₂不平行．
点评：反证法证明问题，是常见的证明方法，关键是找出与已知相矛盾的条件．