Question

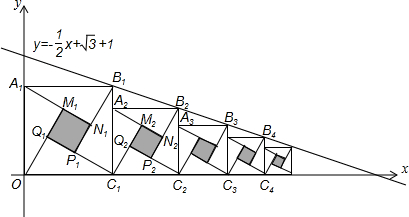
由四个全等的直角三角形围成一个大正方形，中间的阴影部分是一个小正方形的“赵爽弦图”，若这四个全等的直角三角形有一个角为30°，顶点B₁，B₂，B₃，…，B_n和C₁，C₂，C₃，…，C_n分别在直线y=-

1

2

x+

3

+1和x轴上，则第一个阴影正方形的面积为

4

9

，第n个阴影正方形的面积为

(

4

9

)n

．

Answer 1

分析：首先设B₁点坐标为（t，t），由顶点B₁在直线y=-

1

2

x+

3

+1上，即可求得t的值，又由这四个全等的直角三角形有一个角为30°，可求得第一个阴影正方形的边长，则可求得第一个阴影正方形的面积；可设正方形A₂B₂C₂C₁的边长为a，第一个阴影正方形与第二个阴影正方形的相似比为：a：t=2：3，即可求得答案．

解答：解：如图：设B₁点坐标为（t，t），
∴t=-

1

2

t+

3

+1，
解得：t=

2

3

（

3

+1），
∴A₁B₁=t=

2

3

（

3

+1），
∵这四个全等的直角三角形有一个角为30°，
∴B₁N₁=

1

2

A₁B₁=

1

2

t=

1

3

（

3

+1），A₁N₁=A₁B₁•cos30°=

3

2

t=

3

2

×

2

3

（

3

+1）=

3+ 3

3

，
∴B₁P₁=A₁N₁=

3+ 3

3

，
∴N₁P₁=B₁P₁-B₁N₁=

3+ 3

3

-

3 +1

3

=

2

3

，
∴第一个阴影正方形的面积是：（

2

3

）²=

4

9

；
设正方形A₂B₂C₂C₁的边长为a，
∵直线y=-

1

2

x+

3

+1的斜率为-

1

2

，
∴tan∠B₁B₂A₂=

A2B1

A2B2

=

1

2

，
在Rt△A₂B₂B₁中，

A2B2

A2B1

=

a

t-a

=2，
∴a：t=2：3，
∵N₁P₁=B₁P₁-B₁N₁=（

3

2

-

1

2

）t，
同理：N₂P₂=B₂P₂-B₂N₂=（

3

2

-

1

2

）a，
∴第一个阴影正方形与第二个阴影正方形的相似比为：a：t=2：3，
∴第一个阴影正方形与第二个阴影正方形的面积比为4：9，
∴第二个阴影正方形的面积为：

4

9

×

4

9

=（

4

9

）²，
∴第三个阴影正方形的面积为：

4

9

×

4

9

×

4

9

=（

4

9

）³，
∴第n个阴影正方形的面积为：（

4

9

）ⁿ．
故答案为：

4

9

，（

4

9

）ⁿ．

点评：此题主要考查了正方形的性质、含30°角的直角三角形的性质、相似多边形的性质以及一次函数的综合应用．此题难度较大，注意掌握数形结合思想与方程思想的应用．