Question

如图，一个用卡纸做成的圆饼状图形放置在V形架中．CA和CB都是⊙O的切线，切点分别是A，B．如果⊙O的半径为cm，且AB=6cm，
（1）求∠ACB的度数．
（2）若将扇形AOB做成一个圆锥，求此圆锥底面圆半径．

Answer 1

解：（1）如图，连接OC交AB于点D． …（1分）
∵CA，CB分别是⊙O的切线，
∴CA=CB，OC平分∠ACB，∴OC⊥AB． …（2分）
∵AB=6，∴BD=3．在Rt△OBD中，∵，
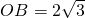∴，∴∠BOD=60°．…（3分）
∵B是切点，∴OB⊥BC，∴∠OCB=30°，
∴∠ACB=60°．…（4分）

（2）AB==…（5分）
设底圆半径为r，则2πr=r=…（6分）
分析：（1）连接OC交AB于点D，那么我们不难得出BD是AB的一半，CD平分∠ACB，那么只要求出∠COB的度数就能求出∠ACB的度数，已知了OB的长，BD（AB的一半）的长，这样在直角三角形ODB中根据三角形函数我们不难得出∠DOB的值，也就能求出∠ACB的度数了．
（2）首先求得弧AB的长，然后利用底面周长等于弧长求得半径即可．
点评：本题主要考查切线的性质，解直角三角形及圆锥的计算等知识点，通过构建直角三角形来求度数是比较常用的方法．