Question

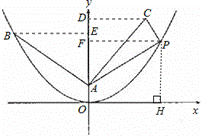
如图，在直角坐标系中，已知点A（0，1），B（-4，4），将点B绕点A顺时针方向90°得到点C；顶点在坐标原点的拋物线经过点B．

（1）求抛物线的解析式和点C的坐标；

（2）抛物线上一动点P，设点P到x轴的距离为，点P到点A的距离为，试说明；

（3）在（2）的条件下，请探究当点P位于何处时，△PAC的周长有最小值，并求出△PAC的周长的最小值．

解：

Answer 1

解：（1）设抛物线的解析式：，

∵拋物线经过点B（-4，4），

∴4=a•4²，解得a=，

所以抛物线的解析式为：；

过点B作BE⊥y轴于E，过点C作CD⊥y轴于D，如图，

∵点B绕点A顺时针方向90°得到点C，

∴Rt△BAE≌Rt△ACD，

∴AD=BE=4，CD=AE=OE-OA=4-1=3，

∴OD=AD+OA=5，

∴C点坐标为（3，5）；

（2）设P点坐标为（a，b），过P作PF⊥y轴于F，PH⊥x轴于H，如图，

∵点P在抛物线上，

∴，

∴，

∵AF=OF-OA=PH-OA=，PF=a，

在Rt△PAF中，PA=，

∴；

（3）由（1）得AC=5，

∴△PAC的周长=PC+PA+5

=PC+PH+6，

要使PC+PH最小，则C、P、H三点共线，

∴此时P点的横坐标为3，把x=3代入，得到，

即P点坐标为（3，），此时PC+PH=5，

∴△PAC的周长的最小值=5+6=11．