题目内容
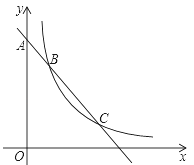
【题目】如图1，点A和点B分别在y轴正半轴和x轴负半轴上，且OA=OB，点C和点D分别在第四象限和第一象限，且OC⊥OD，OC=OD，点D的坐标为（m，n），且满足
+|n﹣2|=0．
（1）求点D的坐标；（2）求∠AKO的度数；（3）如图2，点P，Q分别在y轴正半轴和x轴负半轴上，且OP=OQ，直线ON⊥BP交AB于点N，MN⊥AQ交BP的延长线于点M，判断ON，MN，BM的数量关系并证明．
【答案】(1)(4,2);(2)135°;(3)见解析.
【解析】
（1）利用非负数的性质即可解决问题；（2）如图1中，作OE⊥BD于E，OF⊥AC于F．只要证明△BOD≌△AOC，推出EO=OF（全等三角形对应边上的高相等），推出OK平分∠BKC，再证明∠AKB=∠BOA=90°，即可解决问题；（3）结论：BM=MN+ON；只要证明△BNH≌△BNO，以及MH=MB即可解决问题；
解：（1）∵
=0，
又∵
≥0，|n﹣2|≥0，
∴n=2，m=4，
∴点D坐标为（4，2）．
（2）如图1中，作OE⊥BD于E，OF⊥AC于F．
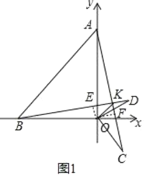
∵OA=OB，OD=OC，∠AOB=∠COD=90°，
∴∠BOD=∠AOC，
∴△BOD≌△AOC，
∴EO=OF（全等三角形对应边上的高相等），
∴OK平分∠BKC，
∴∠OBD=∠OAC，易证∠AKB=∠BOA=90°，
∴∠OKE=45°，
∴∠AKO=135°．
（3）结论：BM=MN+ON．
理由：如图2中，过点B作BH∥y轴交MN的延长线于H．
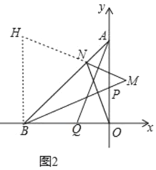
∵OQ=OP，OA=OB，∠AOQ=∠BOP=90°，
∴△AOQ≌△BOP，
∴∠OBP=∠OAQ，
∵∠OBA=∠OAB=45°，
∴∠ABP=∠BAQ，
∵NM⊥AQ，BM⊥ON，
∴∠ANM+∠BAQ=90°，∠BNO+∠ABP=90°，
∴∠ANM=∠BNO=∠HNB，
∵∠HBN=∠OBN=45°，BN=BN，
∴△BNH≌△BNO，
∴HN=NO，∠H=∠BON，
∵∠HBM+∠MBO=90°，∠BON+∠MBO=90°，
∴∠HBM=∠BON=∠H，
∴MH=MB，
∴BM=MN+NH=MN+ON．
