题目内容
(I组)已知⊙O的半径为3,P是⊙O外一点,OP的长为5,PA是⊙O的切线,A为切点,那么PA的长等于 .(II组)已知向量
 与向量
与向量 是互为相反的向量,如果
是互为相反的向量,如果 ,那么k= .
,那么k= .
【答案】分析:(I组)连接OA,由切线的性质知OA⊥AP,而OP=5,OA=3,所以利用勾股定理可以求得PA的长度;
(II组)根据互为相反向量的知识知 +
+ =0,即可求得k的值.
=0,即可求得k的值.
解答: (I组)解:如图,连接OA,
(I组)解:如图,连接OA,
∵PA是⊙O的切线,切点为A,
∴OA⊥AP,
∵OP=5,OA=3,
∴PA=4(勾股定理);
(II组)∵向量 与向量
与向量 是互为相反的向量,
是互为相反的向量,
∴ +
+ =0;
=0;
∴ =-
=- ,
,
∴如果 ,那么k=-1;
,那么k=-1;
故答案是:(I组)4;(II组)-1.
点评:本题考查了圆的切线性质,平面向量.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
(II组)根据互为相反向量的知识知
 +
+ =0,即可求得k的值.
=0,即可求得k的值.解答:
 (I组)解:如图,连接OA,
(I组)解:如图,连接OA,∵PA是⊙O的切线,切点为A,
∴OA⊥AP,
∵OP=5,OA=3,
∴PA=4(勾股定理);
(II组)∵向量
 与向量
与向量 是互为相反的向量,
是互为相反的向量,∴
 +
+ =0;
=0;∴
 =-
=- ,
,∴如果
 ,那么k=-1;
,那么k=-1;故答案是:(I组)4;(II组)-1.
点评:本题考查了圆的切线性质,平面向量.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
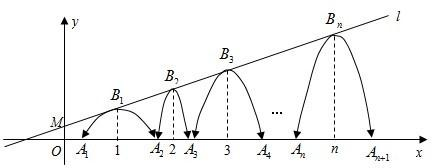
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
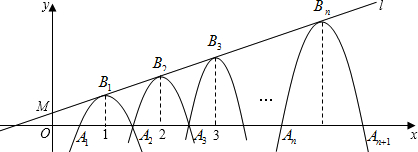
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).