Question

反比例函数y=

6

x

与y=

3

x

在第一象限的图象如图所示，作一条平行于x轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为

1.5

．

Answer 1

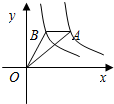
分析：由于AB∥x轴，可知AB两点的纵坐标相等，于是可设A点坐标是（a，c），B点坐标是（b，c），于是可得

6

a

=

3

b

，即b=

1

2

a，进而可求AB，据图可知△AOB的高是c，再利用面积公式可求其面积．

解答：解：由于AB∥x轴，设A点坐标是（a，c），B点坐标是（b，c），那么

6

a

=

3

b

，
∴b=

1

2

a，
∴AB=|a-b|=

1

2

a，
∵c=

6

a

，
∴S_△AOB=

1

2

AB•c=

1

2

×

1

2

a×

6

a

=

3

2

，
故答案是

3

2

．

点评：本题考查了反比例函数系数k的几何意义，解题的关键是注意A、B两点的纵坐标相等．