题目内容
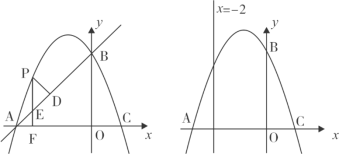
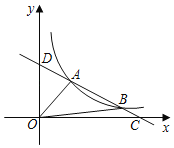
【题目】如图,点A(m,3)、B(6,n)在双曲线y=![]() (x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(x>0)上,直线y=ax+b经过A、B两点,并与x轴、y轴分别相交手C、D两点,已知S△OAB=8.
(1)求双曲线y=![]() 的函数表达式;
的函数表达式;
(2)求△COD的周长;
(3)直接写出不等式![]() -ax>b的解集.
-ax>b的解集.
【答案】(1)y=![]() ;(2)12+4
;(2)12+4![]() ;(3)0<x<2或x>6.
;(3)0<x<2或x>6.
【解析】
(1)把A(m,3)、B(6,n)代入双曲线y=![]() ,可得m=2n,再根据S△OAB=8,求出m、n,确定点A、B的坐标,进而确定反比例函数的关系式;
,可得m=2n,再根据S△OAB=8,求出m、n,确定点A、B的坐标,进而确定反比例函数的关系式;
(2)求出直线y=ax+b的关系式,进一步得到一次函数与x轴、y轴的交点坐标,得到OC、OD的长,再利用勾股定理求出CD,可求出三角形的周长;
(3)根据一次函数与反比例函数的图象交点和图象位置直观判断即可.
解:(1)A(m,3)、B(6,n)在双曲线y=![]() 图象上,
图象上,
∴3m=6n=k,
∴m=2n,
如图,过点A、B分别作AM⊥OC,BN⊥OC,垂足为M、N,

∵S四边形AONB=S△AOM+S梯形AMNB=S△AOB+S△BON,S△AOM=S△BON=|k|,
∴S梯形AMNB=S△AOB=8,
即:![]() (3+n)(6﹣m)=8,
(3+n)(6﹣m)=8,
∴n=1,m=2,(负值已舍去)
∴点A(2,3),B(6,1),
∴k=6,
∴反比例函数表达式为y=![]() ,
,
(2)把点A(2,3),B(6,1)代入直线y=ax+b得,
![]() ,解得,a=﹣
,解得,a=﹣![]() ,b=4,
,b=4,
∴一次函数的关系式为y=﹣![]() x+4,
x+4,
当x=0时,y=4,∴点D(0,4),即OD=4,
当y=0时,即﹣![]() x+4=0,解得x=8,∴点C(8,0),即OC=8,
x+4=0,解得x=8,∴点C(8,0),即OC=8,
∴CD=![]() =4
=4![]() ,
,
∴△COD的周长为4+8+4![]() =12+4
=12+4![]() ;
;
(3)不等式![]() -ax>b,就是不等式
-ax>b,就是不等式![]() >ax+b,
>ax+b,
即:反比例函数的值大于一次函数的值时,自变量的取值范围,
由图象可知,0<x<2或x>6,
答:不等式![]() -ax>b的解集为0<x<2或x>6.
-ax>b的解集为0<x<2或x>6.

 发散思维新课堂系列答案
发散思维新课堂系列答案