��Ŀ����
����Ŀ����ͼ�ף�ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C������B��C�����������y=x2+bx+c��x�����һ������ΪA������ΪP��
��1����������ߵĽ���ʽ��
��2���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ��C��P��MΪ�����������Ϊ���������Σ������ڣ���ֱ��д�������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��3����0��x��3ʱ��������������һ��E��ʹ��CBE����������ֵ��ͼ�ҡ�������ͼ̽������
���𰸡�
��1��
�⣺��ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C��
��B��3��0����C��0��3����
��B��C������������߽���ʽ�ɵ� ![]() �����
����� ![]() ��
��
�������߽���ʽΪy=x2��4x+3
��2��
�⣺��y=x2��4x+3=��x��2��2��1��
�������߶Գ���Ϊx=2��P��2����1����
��M��2��t������C��0��3����
��MC= ![]() =
= ![]() ��MP=|t+1|��PC=
��MP=|t+1|��PC= ![]() =2
=2 ![]() ��
��
�ߡ�CPMΪ���������Σ�
����MC=MP��MC=PC��MP=PC���������
�ٵ�MC=MPʱ������ ![]() =|t+1|�����t=
=|t+1|�����t= ![]() ����ʱM��2��
����ʱM��2�� ![]() ����
����
�ڵ�MC=PCʱ������ ![]() =2
=2 ![]() �����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
�����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
�۵�MP=PCʱ������|t+1|=2 ![]() �����t=��1+2
�����t=��1+2 ![]() ��t=��1��2
��t=��1��2 ![]() ����ʱM��2����1+2
����ʱM��2����1+2 ![]() ����2����1��2
����2����1��2 ![]() ����
����
���Ͽ�֪�������������ĵ�M��������Ϊ��2�� ![]() ����2��7����2����1+2
����2��7����2����1+2 ![]() ����2����1��2
����2����1��2 ![]() ��
��
��3��
�⣺��ͼ����E��EF��x�ᣬ��BC�ڵ�F����x���ڵ�D��
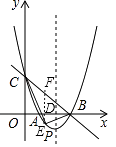
��E��x��x2��4x+3������F��x����x+3����
��0��x��3��
��EF=��x+3����x2��4x+3��=��x2+3x��
��S��CBE=S��EFC+S��EFB= ![]() EFOD+
EFOD+ ![]() EFBD=
EFBD= ![]() EFOB=
EFOB= ![]() ��3����x2+3x��=��
��3����x2+3x��=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
�൱x= ![]() ʱ����CBE��������ʱE������Ϊ��
ʱ����CBE��������ʱE������Ϊ�� ![]() ����
���� ![]() ����
����
����E�������� ![]() ����
���� ![]() ��ʱ����CBE��������
��ʱ����CBE��������
����������1����ֱ�߽���ʽ�����B��C���꣬���ô���ϵ��������������߽���ʽ����2���������߽���ʽ�����P�����꼰�Գ��ᣬ�����M�����꣬��ʾ��MC��MP��PC�ij�����MC=MP��MC=PC��MP=PC����������ɷֱ�õ�����M������ķ��̣������M������ꣻ��3����E��EF��x�ᣬ��ֱ��BC�ڵ�F����x���ڵ�D�������E�����꣬��ʾ��F������꣬��ʾ��EF�ij�����һ���ɱ�ʾ����CBE����������ö��κ��������ʿ������ȡ�����ֵʱE������꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�






