题目内容
已知:关于x,y的方程组
|
(1)求m的取值范围;
(2)设方程组的两个实数解为
|
|
分析:(1)根据判别式大于零即可求出m的取值范围;
(2)根据根与系数的关系即可求出m的值;
(2)根据根与系数的关系即可求出m的值;
解答:解:(1)∵x,y的方程组
,
∴m2x2+2mx+4x+1=0,
∵方程组有两个实数解,∴△=(2m+4)2-4m2>0,解得:m>-1且m≠0;
(2)∵y2-2y+1+
=0,
∴y2+(
-2)y+1-
=0,
∵y1•y2=-7,y1•y2=1-
=-7,
∴m=1.
|
∴m2x2+2mx+4x+1=0,
∵方程组有两个实数解,∴△=(2m+4)2-4m2>0,解得:m>-1且m≠0;
(2)∵y2-2y+1+
| 4(y-2) |
| m |
∴y2+(
| 4 |
| m |
| 8 |
| m |
∵y1•y2=-7,y1•y2=1-
| 8 |
| m |
∴m=1.
点评:本题考查了高次方程及根的判别式,难度一般,关键是根据根与系数的关系求m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数据1,2,3,3,4,5,则下列关于这组数据的说法错误的是( )
| A、平均数、中位数和众数都是3 | ||||
| B、极差为4 | ||||
| C、方差为10 | ||||
D、标准差是
|
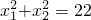 ,求m的值.
,求m的值.