题目内容
如图，两个同心圆O，大圆的弦AB切小圆于C，且AB=6，则圆环（阴影）的面积为________（保留π）
9π
分析：连接OC，OA，利用垂径定理即可求得AC的长，根据圆环（阴影）的面积=π•OA2-π•OC2=π（OA2-OC2），以及勾股定理即可求解．
解答：
解：连接OC，OA，
∵AB切小圆O于C，
∴OC⊥AB，∴AC=
AB=3，
∴S阴影=π•OA2-π•OC2
=π（OA2-OC2）
=π•AC2
=9π．
故答案为：9π．
点评：本题考查了垂径定理，切线的性质，以及勾股定理，解题的关键是正确作出辅助线，注意到圆环（阴影）的面积=π•OA2-π•OC2=π（OA2-OC2），利用勾股定理把圆的半径之间的关系转化为直角三角形的边的关系．
分析：连接OC，OA，利用垂径定理即可求得AC的长，根据圆环（阴影）的面积=π•OA2-π•OC2=π（OA2-OC2），以及勾股定理即可求解．
解答：
解：连接OC，OA，∵AB切小圆O于C，
∴OC⊥AB，∴AC=
AB=3，∴S阴影=π•OA2-π•OC2
=π（OA2-OC2）
=π•AC2
=9π．
故答案为：9π．
点评：本题考查了垂径定理，切线的性质，以及勾股定理，解题的关键是正确作出辅助线，注意到圆环（阴影）的面积=π•OA2-π•OC2=π（OA2-OC2），利用勾股定理把圆的半径之间的关系转化为直角三角形的边的关系．
练习册系列答案
相关题目
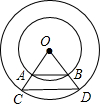如图，两个同心圆的圆心为O，大圆的半径OC、OD交小圆于A、B，试探究AB与CD有怎样的位置关系？
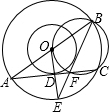如图，两个同心圆的圆心是O，AB是大圆的直径，大圆的弦与小圆相切于点D，连接OD并延长交大圆于点E，连接BE交AC于点F，已知AC=
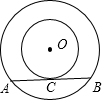如图，两个同心圆中，大圆的弦AB切小圆于点C，已知大圆的半径为5，小圆的半径为3，那么AB长是
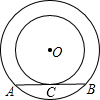如图，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB=（ ）
（1997•重庆）如图．两个同心圆，小圆的切线被大圆截得的部分为AB，两圆所围成的圆环面积是9π，则AB=