题目内容
如图，在Rt△ADC中，∠ADC=90°，以CD为直径的⊙O交AC于点E，点G是AD的中点． 求证：GE是⊙O的切线．
证明：连接OE，
∵CD是⊙O的直径，
∴∠CED=90°，
∴∠AED=90°，
又G为AD的中点，
∴EG=
AD=DG，
∴∠GED=∠GDE，
∵OE=OD，
∴∠OED=∠ODE，
∴∠GED+∠OED=∠GDE+∠ODE，
即∠OEG=∠ODG，
∵∠ODG=90°，
∴∠OEG=90°，
∴GE为⊙O的切线．
∵CD是⊙O的直径，
∴∠CED=90°，
∴∠AED=90°，
又G为AD的中点，
∴EG=
AD=DG，∴∠GED=∠GDE，
∵OE=OD，
∴∠OED=∠ODE，
∴∠GED+∠OED=∠GDE+∠ODE，
即∠OEG=∠ODG，
∵∠ODG=90°，
∴∠OEG=90°，
∴GE为⊙O的切线．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
（2012•和平区二模）如图，在Rt△ADC中，∠ADC=90°，以CD为直径的半圆O交AC于点E，点G是AD的中点．
如图，在Rt△ADC中，∠ADC=90°，以CD为直径的⊙O交AC于点E，点G是AD的中点．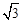
，点B为CD延长线上一点，且BD＝2AD．求AB的长.
如图，在Rt△ADC中，∠ADC=90°，以CD为直径的⊙O交AC于点E，点G是AD的中点．