题目内容
如图,在▱ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
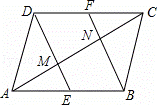
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵E、F分别是AB、CD的中点,
∴BE=DF,
∵BE∥DF,
∴四边形EBFD为平行四边形;
(2)证明:∵四边形EBFD为平行四边形,
∴DE∥BF,
∴∠CDM=∠CFN.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAC=∠DCA,∠ABN=∠CFN,
∴∠ABN=∠CDM,
在△ABN与△CDM中,
 ,
,
∴△ABN≌△CDM (ASA).

练习册系列答案
相关题目
下列各图中,∠1与∠2互为余角的是( )
|
| A. |
| B. |
| C. |
| D. |
|




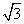 ,将△BOC绕C点顺
,将△BOC绕C点顺 时针方向旋转到△AQC的位置,则∠AQ
时针方向旋转到△AQC的位置,则∠AQ C= .
C= .

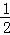 x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.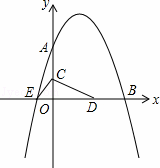

 )÷
)÷ -
- ,其中a取=1、0、1、2中的—个数。
,其中a取=1、0、1、2中的—个数。