题目内容
如图，PA切⊙O于A点，C是弧AB上任意一点，∠PAB=58°，则∠C的度数是________度．
122
分析：若要利用弦切角的度数，需构造圆周角．在优弧AB上任取一点D，连接AD、BD；根据弦切角定理，易得∠D=∠PAC=58°；而四边形ACBD正好是⊙O的内接四边形，根据圆内接四边形对角互补，可求出∠C的度数．
解答：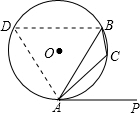
解：在优弧AB上任意找一点D，连接AD、BD；
∵PA与⊙O相切，切点为A，
∴∠D=∠PAB=58°，
∵四边形ACBD内接于⊙O，
∴∠C+∠D=180°，即∠C=122°．
点评：此题综合考查了弦切角定理和圆内接四边形的性质．
分析：若要利用弦切角的度数，需构造圆周角．在优弧AB上任取一点D，连接AD、BD；根据弦切角定理，易得∠D=∠PAC=58°；而四边形ACBD正好是⊙O的内接四边形，根据圆内接四边形对角互补，可求出∠C的度数．
解答：
解：在优弧AB上任意找一点D，连接AD、BD；∵PA与⊙O相切，切点为A，
∴∠D=∠PAB=58°，
∵四边形ACBD内接于⊙O，
∴∠C+∠D=180°，即∠C=122°．
点评：此题综合考查了弦切角定理和圆内接四边形的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
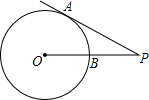如图，PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，则⊙O的半径为（ ）A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
如图，PA切⊙O于点A，PBC是⊙O的割线，且PB=BC，如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
8、如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA=4，PB=2，则⊙O的半径等于（ ）
如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
如图：PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中错误的是（ ）