题目内容
如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm

伞架 DE DF AE AF AB AC
长度 36 36 36 36 86 86
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm).
备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
【答案】
(1)72cm(2)44cm
【解析】解:(1)由题意,得AM=AE+DE=36+36=72(cm).
∴AM的长为72cm。
(2)∵AP平分∠BAC,∠BAC=104°,∴∠EAD= ∠BAC=52°。
∠BAC=52°。
过点E作EG⊥AD于G,
∵AE=DE=36,∴AG=DG,AD=2AG。
在△AEG中,∵∠AGE=90°,
∴AG=AE?cos∠EAG=36?cos52°=36×0.6157=22.1652。
∴AD=2AG=2×22.1652≈44(cm)。
∴AD的长约为44cm。

(1)根据AM=AE+DE求解即可。
(2)先根据角平分线的定义得出∠EAD= ∠BAC=52°,再过点E作EG⊥AD于G,由等腰三角形的性质得出AD=2AG,然后在△AEG中,利用余弦函数的定义求出AG的长,进而得到AD的长度。
∠BAC=52°,再过点E作EG⊥AD于G,由等腰三角形的性质得出AD=2AG,然后在△AEG中,利用余弦函数的定义求出AG的长,进而得到AD的长度。

练习册系列答案
相关题目
如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm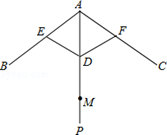
| 伞架 | DE | DF | AE | AF | AB | AC |
| 长度 | 36 | 36 | 36 | 36 | 86 | 86 |
(2)当∠BAC=104°时,求AD的长(精确到1cm).
备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.
 我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,△AED与△AFD始终保持全等,因此伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.你知道△AED≌△AFD的理由吗?( )
我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,△AED与△AFD始终保持全等,因此伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.你知道△AED≌△AFD的理由吗?( ) (2013•绍兴)如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
(2013•绍兴)如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm