题目内容
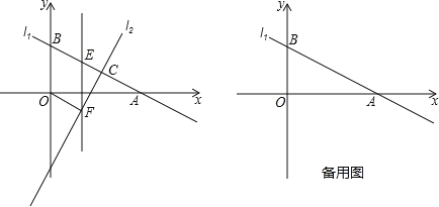
【题目】如图，在平面直角坐标系中，△ABC 是等腰直角三角形，∠ABC=90°，AB平行x 轴，点C在 x 轴上，若点A，B分别在正比例函数 y=6x 和 y=kx 的图象上，则 k=__________．
【答案】
【解析】
根据点A在正比例函数 y=6x的图像上，设点A为（x，6x），由AB平行x 轴，AB=BC，可以得到点B的坐标为：（7x，6x），代入计算，即可求出k的值.
解：∵点A在正比例函数 y=6x的图像上，
则设点A为（x，6x），
∵由AB平行x 轴，
∴点B的纵坐标为6x，
∵△ABC是等腰直角三角形，∠ABC=90°，
∴AB=BC=6x，
∴点B的横坐标为：7x，
即点B为：（7x，6x），
把点B代入y=kx，则
，
∴
；
故答案为：.
练习册系列答案
阅读快车系列答案
相关题目
