题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,菱形
为坐标原点,菱形![]() 的对角线
的对角线![]() 在
在![]() 轴上,
轴上,![]() 两点分别在第一象限和第四象限.直线
两点分别在第一象限和第四象限.直线![]() 的解析式为
的解析式为![]() .
.

(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,![]() 为射线
为射线![]() 上一动点(不与点
上一动点(不与点![]() 和点
和点![]() 重合),过点
重合),过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() .设线段
.设线段![]() 的长度为
的长度为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)如图3,在(2)的条件下,当点![]() 运动到线段
运动到线段![]() 的延长线上时,连接
的延长线上时,连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,的角平分线
,的角平分线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)A(4,2);(2)d=![]() ;(3)S(
;(3)S(![]() ,0).
,0).
【解析】
(1)如图1中,连接AC交OB于F,延长BA交y轴于E.利用三角形的中位线定理解决问题即可.
(2)分两种情形:①如图2-1中,当0<m<4时,作PM⊥OB于M,QN⊥OB于N.②如图2-2中,当m>4时,作PM⊥OB于M,QN⊥OB于N.分别求解即可.
(3)如图3中,连接AC交OB于K,在KB上取一点J,使得AK=JK,连接AJ,作ET⊥OB于T,延长PE交y轴于R,连接FM交ES于L.首先证明AJ平分∠BAM,设KM=a,利用角平分线的性质定理构建方程求出a,可得点M的坐标,即可解决问题.
(1)如图1中,连接AC交OB于F,延长BA交y轴于E.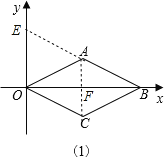
∵直线AB的解析式为y=-![]() x+4,
x+4,
∴E(0,4),B(8,0),
∴OE=4,OB=8,
∵四边形OABC是菱形,
∴AC⊥OB,OF=FB=4,
∴∠AFB=∠EOB=90°,
∴AF∥OE,∵OF=FB,
∴AE=AB,
∴AF=![]() OE=2,
OE=2,
∴A(4,2).
(2)如图2-1中,当0<m<4时,作PM⊥OB于M,QN⊥OB于N.
∵PQ∥OB,PM⊥OB,QN⊥OB,
∴PM=QN,∠OMP=∠BNQ=90°,四边形PQNM是矩形,
∴PQ=MN
∵AO=AB,
∴∠POM=∠QBN,
∴△PMO≌△QNB(AAS),
∴OM=BN=m,
∴d=PQ=MN=8-2m.
如图2-2中,当m>4时,作PM⊥OB于M,QN⊥OB于N.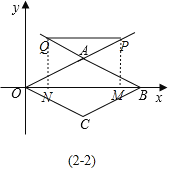
同法可得PQ=MN,OM=BM=m,
∴d=PQ=MN=2m-8.
综上所述,d=![]() .
.
(3)如图3中,连接AC交OB于K,在KB上取一点J,使得AK=JK,连接AJ,作ET⊥OB于T,延长PE交y轴于R,连接FM交ES于L.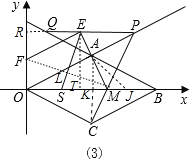
∵AK=KJ,∠AKJ=90°,
∴∠AJK=45°,
∵∠AJK=∠JA+∠ABJ=45°,![]() ∠BAM+∠AOB=
∠BAM+∠AOB=![]() ∠BAM+∠ABO=45°,
∠BAM+∠ABO=45°,
∴∠BAJ=![]() ∠BAM,
∠BAM,
∴AJ平分∠MAB,
∴![]() (角平分线的性质定理,可以用面积法证明,见下面补充说明),
(角平分线的性质定理,可以用面积法证明,见下面补充说明),
设KM=a,则AM=![]() ,MJ=2-a,JB=2,AB=2
,MJ=2-a,JB=2,AB=2![]() ,
,
∴![]() ,
,
整理得:a2-5a+4=0,
解得a=1或4(舍弃),
∴KM=1,OM=5,
∴M(5.0),
∵C(4,-2),
∴直线CM的解析式为y=2x-10,
∵直线OA的解析式为y=![]() x
x
由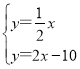 ,解得
,解得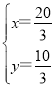 ,
,
∴P(![]() ),
),
∵直线MA的解析式为y=-2x+10,
∵PE∥OB,
∴E(![]() ),
),
∵ER⊥OR,ET⊥OB,
∴∠ERF=∠ETM=∠ROT=90°,
∴ER=RT=![]() ,四边形RETO是正方形,
,四边形RETO是正方形,
∴TM=5-![]() =
=![]() ,
,
∵∠RET=∠MEF=90°,
∴∠FER=∠MET,
∴△ERF≌△ETM(ASA),
∴RF=TM=![]() ,EF=EM,
,EF=EM,
∴OF=![]() -
-![]() =
=![]() ,
,
∴F(0,![]() ),
),
∵EF=EM,ES平分∠FEM,
∴ES⊥FM,
∴FL=LM,
∴L(![]() ),
),
∴直线ES的解析式为y=3x-![]() ,
,
令y=0,得到x=![]() ,
,
∴S(![]() ,0).
,0).
补充说明:如图,AJ平分∠MAB,则![]() ,
,
理由:作JE⊥AB于E,JF⊥AM交AM的延长线于F.
∵AJ平分∠MAB,
∴EJ=JF,
∴
∴![]() .
.

 期末集结号系列答案
期末集结号系列答案【题目】抛物线![]() 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.