Question

【题目】如图，已知，直线分别交、于点，，，.

（1）已知，求；

（2）求证：平分；

（3）若，则的度数为______.

Answer 1

【答案】（1）20°；（2）证明见解析；（3）60°.

【解析】

（1）根据平行线的性质可得∠DFG=20°，再由FH⊥FB可求出∠DFH；

（2）延长BF至Q，可证明∠BFE=∠GFC，根据平行线的性质可得∠BFD=∠GFC，利用∠HFG+∠GFQ=∠HFD+∠DFB=90°可证明出结论；

（3）由得，从而求出∠DFB=30°，进而得出∠DFH=60°，由角的平分线的定义可得结论.

（1）∵AB∥CD，

∴∠DFB=∠B，

∵∠B=20°，

∴∠DFB=20°

∵FH⊥FB.

∴∠HFB=90°，即∠HFD+∠DFB=90°，

∴∠HFD =90°-∠DFB=90°-20°=70°；

（2）延长BF至Q，则∠BFE=∠GFQ，如图，

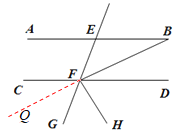
∵HF⊥BF，

∴HF⊥FQ，

∴∠HFG+∠GFQ=90°，

∵AB∥CD，

∴∠B=∠DFB，

∵∠EFB=∠B，

∴∠DFB=∠BFE，

∴∠GFQ=∠DFB，

∵∠HFD+∠DFB=90°，

∴∠HFG=∠HFD，即FH平分∠GFD；

（3）∵AB∥CD，

∴∠DFB=∠B，

∵∠EFB=∠B，

∴∠DFB=∠EFB=∠B

∵

∴

∵，

∴∠DFB=60°，

∴∠BFE=30°，

∴∠GFQ=30°，

∵∠HFQ=90°，

∴∠HFG=90°-∠GFQ=90°-30°=60°.