题目内容
已知, ,
, 是
是 的平分线,点P在
的平分线,点P在 上,
上, .将三角板的直角顶点放置在点P处,绕着点P旋转,CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
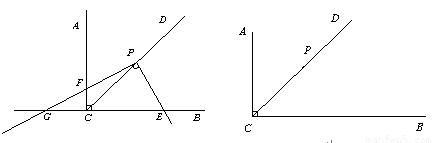
(1)如图9,当点F在射线CA上时,①求证: PF = PE.②设CF= x,EG=y,求y与x的函数解析式并写出函数的定义域.
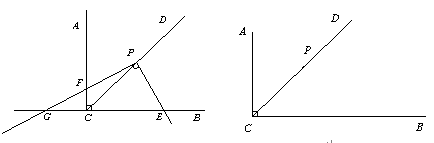
(2)联结EF,当△CEF与△EGP相似时,求EG的长.


 ,
, 是
是 的平分线,点P在
的平分线,点P在 上,
上, .将三角板的直角顶点放置在点P处,绕着点P旋转,CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.
.将三角板的直角顶点放置在点P处,绕着点P旋转,CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.(1)如图9,当点F在射线CA上时,①求证: PF = PE.②设CF= x,EG=y,求y与x的函数解析式并写出函数的定义域.
(2)联结EF,当△CEF与△EGP相似时,求EG的长.


(1) ①证明:过点P作PM⊥AC,PN⊥BC,垂足分别为M、N.
∵ 是
是 的平分线,
的平分线,
∴PM=PN.
由 ,
,
得 .
.
∴ .
.
∵ ,
,
∴ .
.
∴△PMF≌△PNE.
∴PF=PE.

②解:
∵ ,
,
∴ .
.
∵△PMF≌△PNE,
∴ .
.
∴ .
.
∵CF∥PN,
∴ .
.
∴ .
.
∴ (0≤x<1).
(0≤x<1).

(2)当△CEF与△EGP相似时,点F的位置有两种情况:
①当点F在射线CA上时,
∵ ,
, ,
,
∴ .
.
∴ .
.
∴ .
.
在Rt△EGP中, .
.

②当点F在AC延长线上时,
∵ ,
, ,
,
∴ .
.
∵ ,
, ,
,
∴ .
.
易证 ,
,
可得 .
.
∴ .
.
∴ .
.
易证△PMF≌△PNE,
可得 .
.
∵CF∥PN,
∴ .
.
∴ .
.
∴ .
.

∵
 是
是 的平分线,
的平分线, ∴PM=PN.
由
 ,
,得
 .
. ∴
 .
. ∵
 ,
, ∴
 .
. ∴△PMF≌△PNE.
∴PF=PE.

②解:
∵
 ,
, ∴
 .
. ∵△PMF≌△PNE,
∴
 .
. ∴
 .
. ∵CF∥PN,
∴
 .
. ∴
 .
. ∴
 (0≤x<1).
(0≤x<1). 
(2)当△CEF与△EGP相似时,点F的位置有两种情况:
①当点F在射线CA上时,
∵
 ,
, ,
, ∴
 .
. ∴
 .
. ∴
 .
.在Rt△EGP中,
 .
.
②当点F在AC延长线上时,
∵
 ,
, ,
, ∴
 .
. ∵
 ,
, ,
, ∴
 .
.易证
 ,
,可得
 .
. ∴
 .
. ∴
 .
.易证△PMF≌△PNE,
可得
 .
. ∵CF∥PN,
∴
 .
. ∴
 .
. ∴
 .
. 

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
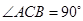 ,
,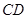 是
是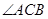 的平分线,点
的平分线,点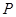 在
在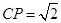 .将三角板的直角顶点放置在点
.将三角板的直角顶点放置在点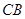 交于点
交于点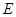 ,另一条直角边与直线
,另一条直角边与直线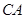 、直线分别交于点
、直线分别交于点 、点
、点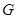 .
.
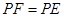 ;
;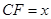 ,
,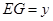 ,求
,求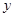 与
与 的函数解析式并写出函数的定义域;
的函数解析式并写出函数的定义域; 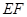 ,当△
,当△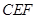 与△
与△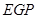 似时,求
似时,求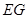 的长.
的长. ,
, 是
是 的平分线,则
的平分线,则 的余角等于 .
的余角等于 .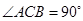 ,
,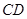 是
是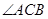 的平分线,点
的平分线,点 在
在 .将三角板的直角顶点放置在点
.将三角板的直角顶点放置在点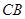 交于点
交于点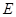 ,另一条直角边与直线
,另一条直角边与直线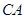 、直线分别交于点
、直线分别交于点 、点
、点 .
.
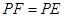 ;
;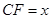 ,
,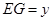 ,求
,求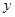 与
与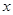 的函数解析式并写出函数的定义域;
的函数解析式并写出函数的定义域; 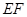 ,当△
,当△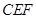 与△
与△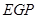 似时,求
似时,求 的长.
的长. ,
, ,
, 是
是 的平分线,
的平分线, ,求
,求 的度数。
的度数。