题目内容
将二次函数y=3（x+2）2-4的图象向右平移3个单位，再向上平移1个单位，所得图象的函数关系式是
- A.y=3（x+5）2-5
- B.y=3（x-1）2-5
- C.y=3（x-1）2-3
- D.y=3（x+5）2-3
C
分析：根据左加右减原则以及抛物线平移不改变a的值得出即可．
解答：原抛物线的顶点为（-2，-4），向右平移3个单位，再向上平移1个单位那么新抛物线的顶点为（1，-3），
可设新抛物线的解析式为：y=3（x-h）2+k，代入得：y=3（x-1）2-3．
故所得的图象的函数关系式为：y=3（x-1）2-3．
故选：C．
点评：此题主要考查了二次函数图象与几何变换，解决本题的关键是得到新抛物线的顶点坐标．
分析：根据左加右减原则以及抛物线平移不改变a的值得出即可．
解答：原抛物线的顶点为（-2，-4），向右平移3个单位，再向上平移1个单位那么新抛物线的顶点为（1，-3），
可设新抛物线的解析式为：y=3（x-h）2+k，代入得：y=3（x-1）2-3．
故所得的图象的函数关系式为：y=3（x-1）2-3．
故选：C．
点评：此题主要考查了二次函数图象与几何变换，解决本题的关键是得到新抛物线的顶点坐标．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
将二次函数y=-2x2+6x-4配成顶点式为（ ）
A、y=-2(x+
| ||||
B、y=-2(x-
| ||||
C、y=-2(x-
| ||||
D、y=-2(x+
|
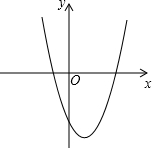（2013•丰台区一模）二次函数y=x2+bx+c的图象如图所示，其顶点坐标为M（1，-4）．