题目内容
如图所示，抛物线y=ax2+bx+c（a≠0）与x轴的两个交点分别为A（-1，0）和B（2，0），当y＜0时，x的取值范围是________．
x＜-1或x＞2
分析：直接从图上可以分析：y＜0时，图象在x轴的下方，共有2部分：一是A的左边，即x＜-1；二是B的右边，即x＞2．
解答：观察图象可知，抛物线与x轴两交点为（-1，0），（2，0），
y＜0，图象在x轴的下方，所以答案是x＜-1或x＞2．
点评：考查了二次函数的图象与函数值之间的联系，函数图象所表现的位置与y值对应的关系，典型的数形结合题型．
分析：直接从图上可以分析：y＜0时，图象在x轴的下方，共有2部分：一是A的左边，即x＜-1；二是B的右边，即x＞2．
解答：观察图象可知，抛物线与x轴两交点为（-1，0），（2，0），
y＜0，图象在x轴的下方，所以答案是x＜-1或x＞2．
点评：考查了二次函数的图象与函数值之间的联系，函数图象所表现的位置与y值对应的关系，典型的数形结合题型．
练习册系列答案
相关题目
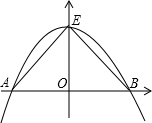如图所示，抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E，且△ABE是等腰直角三角形，AE=BE，则下列关系式中不能成立的是（ ）| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
（2012•河源二模）已知：如图所示，抛物线y=-x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）．
（2012•槐荫区一模）如图所示，抛物线y=x2+bx+c经过A、B两点，A、B两点的坐标分别为（-1，0）、（0，-3）．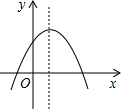
（1997•陕西）如图所示，抛物线对应的函数解析表达式只可能是（ ）
（1997•陕西）如图所示的抛物线是把y=-x2经过平移而得到的．这时抛物线过原点O和x轴正向上一点A，顶点为P；