题目内容
已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.求证:DE是⊙O的切线.

【答案】分析:连接OD,只要证明OD⊥DE即可.此题可运用三角形的中位线定理证OD∥AC,因为DE⊥AC,所以OD⊥DE.
解答: 证明:连接OD.
证明:连接OD.
∵D是BC的中点,O是AB的中点,
∴OD∥AC,
∴∠CED=∠ODE. (4分)
∵DE⊥AC,
∴∠CED=∠ODE=90°. (6分)
∴OD⊥DE,OD是圆的半径,
∴DE是⊙O的切线. (10分)
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.
解答:
 证明:连接OD.
证明:连接OD.∵D是BC的中点,O是AB的中点,
∴OD∥AC,
∴∠CED=∠ODE. (4分)
∵DE⊥AC,
∴∠CED=∠ODE=90°. (6分)
∴OD⊥DE,OD是圆的半径,
∴DE是⊙O的切线. (10分)
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
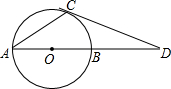 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=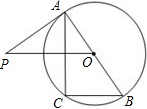 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.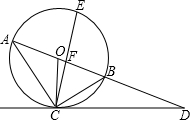

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,