题目内容
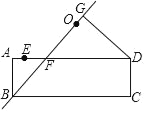
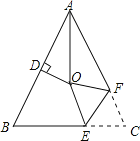
【题目】如图，在
中，
，
，
的平分线与AB的垂直平分线交于点O，将
沿EF折叠，若点C与点O恰好重合，则
______．
【答案】
【解析】
连接OB、OC，根据角平分线的定义求出∠BAO，根据等腰三角形两底角相等求出∠ABC，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB，根据等边对等角可得∠ABO=∠BAO，再求出∠OBC，然后判断出点O是△ABC的外心，根据三角形外心的性质可得OB=OC，再根据等边对等角求出∠OCB=∠OBC，根据翻折的性质可得OE=CE，然后根据等边对等角求出∠COE，再利用三角形的内角和定理列式计算即可
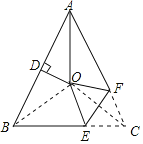
解：如图，连接OB、OC，
，AO为
的平分线，
，
又
，
，
是AB的垂直平分线，
，
，
，
为的平分线，
，
，
点O在BC的垂直平分线上，
又是AB的垂直平分线，
点O是
的外心，
,
，
将
沿
在BC上，F在AC上
折叠，点C与点O恰好重合，
，
，
在
中，
．
故答案为：104°.
练习册系列答案
相关题目
