��Ŀ����
��֪��������ABCD�ı߳�Ϊ1������AE������BC���ڵ�E������AF������CD���ڵ�F����EAF=45°����1����ͼ1������E���߶�BC��ʱ���Բ����߶�EF��BE��DF��������������ϵ����֤����IJ��룮
��2����BE=x��DF=y������E���߶�BC���˶�ʱ����������B��C������ͼ1����y����x�ĺ�������ʽ����ָ��x��ȡֵ��Χ��
��3������E������BC���˶�ʱ�������˵�B������F������CD���˶������ж���EΪԲ����BEΪ�뾶�ġ�E����FΪԲ����FDΪ�뾶�ġ�F֮���λ�ù�ϵ��
��4������E��BC�ӳ�����ʱ����AE��CD���ڵ�G����ͼ2���ʡ�EGF���EFA�ܷ����ƣ��������ƣ����BE��ֵ�������������ƣ���˵�����ɣ�

���𰸡���������1������ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬��֪��F�䡢B��E��һֱ���ϣ�֤��AF��E�ա�AFE���Ӷ��õ�EF=F��E=BE+DF��
��2���ɣ�1���� EF=x+y�ٸ��� CF=1-y��EC=1-x���õ���1-y��2+��1-x��2=��x+y��2�����ɵõ�y= ��0��x��1����
��0��x��1����
��3������E�ڵ�B��C֮��ʱ���ɣ�1��֪ EF=BE+DF���ʴ�ʱ��E���F���У�����E�ڵ�Cʱ��DF=0����F�����ڣ�����E��BC�ӳ�����ʱ������ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬֤�á�AF��E�ա�AFE�����ɵõ�EF=EF��=BE-BF��=BE-FD���Ӷ��õ���ʱ��E���F���У�
��4����EGF���EFA�ܹ����ƣ�ֻҪ����EFG=��EAF=45°���ɣ���ʱ�� CF=CE����BE=x��DF=y���ɣ�3����EF=x-y���� CE2+CF2=EF2���ã�x-1��2+��1+y��2=��x-y��2��
����ɵ� y= ��x��1�������� EC=FC����x-1=1+y����x-1=1+
��x��1�������� EC=FC����x-1=1+y����x-1=1+ �������x2-2x-1=0����֮�������BE�ij���
�������x2-2x-1=0����֮�������BE�ij���
��� �⣺��1�����룺EF=BE+DF���������£�
�⣺��1�����룺EF=BE+DF���������£�
����ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬��֪��F�䡢B��E��һֱ���ϣ���ͼ1��
��AF��=AF��
��F��AE=��1+��3=��2+��3=90°-45°=45°=��EAF��
�� AE=AE��
���AF��E�ա�AFE��
��EF=F��E=BE+DF��
��2���ɣ�1���� EF=x+y
�� CF=1-y��EC=1-x��
�ࣨ1-y��2+��1-x��2=��x+y��2��
����ɵ�y= ��0��x��1����
��0��x��1����
��3���ٵ���E�ڵ�B��C֮��ʱ���ɣ�1��֪ EF=BE+DF���ʴ�ʱ��E���F���У�
�ڵ���E�ڵ�Cʱ��DF=0����F�����ڣ�
�۵���E��BC�ӳ�����ʱ������ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬ͼ2��
�� AF��=AF����1=��2��BF��=FD��
���F��AF=90°��
���F��AE=��EAF=45°��
�� AE=AE��
���AF��E�ա�AFE��
��EF=EF��=BE-BF��=BE-FD��
���ʱ��E���F���У�
��������������E���߶�BC��ʱ����E���F���У�����E��BC�ӳ�����ʱ����E���F���У�
��4����EGF���EFA�ܹ����ƣ�ֻҪ����EFG=��EAF=45°���ɣ�
��ʱ�� CF=CE������1�֣�
��BE=x��DF=y���ɣ�3����EF=x-y��
�� CE2+CF2=EF2���ã�x-1��2+��1+y��2=��x-y��2��
����ɵ� y= ��x��1����
��x��1����
���� EC=FC����x-1=1+y����x-1=1+ �������
�������
x2-2x-1=0����֮��
x=1+ ��x=1-
��x=1- ���������⣬��ȥ����
���������⣬��ȥ����
������BE�ij�Ϊ1+ ��
��
���������⿼���������ε��ۺ�֪ʶ��������Ŀ�������п���ѹ���⣬�ѶȽϴ������������ѧ�ε��ۺ�֪ʶ����ʱ���뺯��֪ʶ���ϣ�������������Ѷȣ�
��2���ɣ�1���� EF=x+y�ٸ��� CF=1-y��EC=1-x���õ���1-y��2+��1-x��2=��x+y��2�����ɵõ�y=
 ��0��x��1����
��0��x��1������3������E�ڵ�B��C֮��ʱ���ɣ�1��֪ EF=BE+DF���ʴ�ʱ��E���F���У�����E�ڵ�Cʱ��DF=0����F�����ڣ�����E��BC�ӳ�����ʱ������ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬֤�á�AF��E�ա�AFE�����ɵõ�EF=EF��=BE-BF��=BE-FD���Ӷ��õ���ʱ��E���F���У�
��4����EGF���EFA�ܹ����ƣ�ֻҪ����EFG=��EAF=45°���ɣ���ʱ�� CF=CE����BE=x��DF=y���ɣ�3����EF=x-y���� CE2+CF2=EF2���ã�x-1��2+��1+y��2=��x-y��2��
����ɵ� y=
 ��x��1�������� EC=FC����x-1=1+y����x-1=1+
��x��1�������� EC=FC����x-1=1+y����x-1=1+ �������x2-2x-1=0����֮�������BE�ij���
�������x2-2x-1=0����֮�������BE�ij������
 �⣺��1�����룺EF=BE+DF���������£�
�⣺��1�����룺EF=BE+DF���������£�����ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬��֪��F�䡢B��E��һֱ���ϣ���ͼ1��
��AF��=AF��
��F��AE=��1+��3=��2+��3=90°-45°=45°=��EAF��
�� AE=AE��
���AF��E�ա�AFE��
��EF=F��E=BE+DF��
��2���ɣ�1���� EF=x+y
�� CF=1-y��EC=1-x��
�ࣨ1-y��2+��1-x��2=��x+y��2��
����ɵ�y=
 ��0��x��1����
��0��x��1������3���ٵ���E�ڵ�B��C֮��ʱ���ɣ�1��֪ EF=BE+DF���ʴ�ʱ��E���F���У�
�ڵ���E�ڵ�Cʱ��DF=0����F�����ڣ�
�۵���E��BC�ӳ�����ʱ������ADF���ŵ�A��˳ʱ�뷽����ת90°���á�ABF�䣬ͼ2��
�� AF��=AF����1=��2��BF��=FD��
���F��AF=90°��
���F��AE=��EAF=45°��
�� AE=AE��
���AF��E�ա�AFE��
��EF=EF��=BE-BF��=BE-FD��
���ʱ��E���F���У�
��������������E���߶�BC��ʱ����E���F���У�����E��BC�ӳ�����ʱ����E���F���У�
��4����EGF���EFA�ܹ����ƣ�ֻҪ����EFG=��EAF=45°���ɣ�
��ʱ�� CF=CE������1�֣�
��BE=x��DF=y���ɣ�3����EF=x-y��
�� CE2+CF2=EF2���ã�x-1��2+��1+y��2=��x-y��2��
����ɵ� y=
 ��x��1����
��x��1�������� EC=FC����x-1=1+y����x-1=1+
 �������
�������x2-2x-1=0����֮��
x=1+
 ��x=1-
��x=1- ���������⣬��ȥ����
���������⣬��ȥ����������BE�ij�Ϊ1+
 ��
�����������⿼���������ε��ۺ�֪ʶ��������Ŀ�������п���ѹ���⣬�ѶȽϴ������������ѧ�ε��ۺ�֪ʶ����ʱ���뺯��֪ʶ���ϣ�������������Ѷȣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
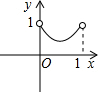
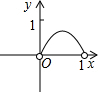
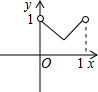
 ��ͼ����֪��������ABCD�߳�Ϊ1��E��F��G��H�ֱ�Ϊ�����ϵĵ㣬��AE=BF=CG=DH����С������EFGH�����Ϊs��AEΪx����s����x�ĺ���ͼ������ǣ�������
��ͼ����֪��������ABCD�߳�Ϊ1��E��F��G��H�ֱ�Ϊ�����ϵĵ㣬��AE=BF=CG=DH����С������EFGH�����Ϊs��AEΪx����s����x�ĺ���ͼ������ǣ�������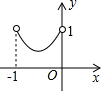
 �ɣ�
�ɣ� s���ٶ��˶���ͬʱ����Q���߶�FC�ϴ�F?C��1cm/s���ٶ��˶�������G��PC�ϣ��ҡ�EGC=��EQC������PD�����˶�ʱ��Ϊt�룮
s���ٶ��˶���ͬʱ����Q���߶�FC�ϴ�F?C��1cm/s���ٶ��˶�������G��PC�ϣ��ҡ�EGC=��EQC������PD�����˶�ʱ��Ϊt�룮 18����ͼ����֪��������ABCD�У�P��BC�ϵ�һ�㣬��AP=DP����֤��P��BC�е㣮
18����ͼ����֪��������ABCD�У�P��BC�ϵ�һ�㣬��AP=DP����֤��P��BC�е㣮 ��ͼ����֪��������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=
��ͼ����֪��������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�DE�ڵ�P����AE=AP=1��PB=