Question

已知梯形两底长分别是3和5，一腰长为4，则另一腰长应满足

 

．

Answer 1

分析：如图，由题意得，AD=3，BC=5，如果作DE∥AB，交BC于点E，则CE=2，在△EDC中，根据三角形的三边关系定理，列出不等式，解答出即可．

解答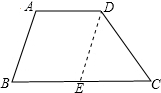：解：如图，由题意得，
作DE∥AB，交BC于点E，
∴AB=DE，
∵AD=3，BC=5，
∴EC=2，
又∵CD=4，
∴在△EDC中，

DE＞CD-EC DE＜CD+EC

，
解得，2＜DE＜6，
即2＜AB＜6．
故答案为：大于2且小于6．

点评：本题主要考查了梯形及三角形的三边关系定理，掌握三角形的两边之和大于第三边，三角形的两边之差小于第三边，是解答本题的关键．