Question

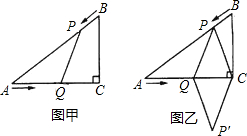
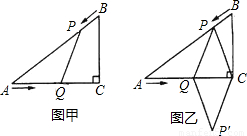
已知：如图①，在Rt△ACB中，∠C=90°，AC=4 cm，BC=3 cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：

（1）当t为何值时，PQ∥BC；

（2）设△AQP的面积为y（cm²），求y与t之间的函数关系式；

（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；

（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

Answer 1

考点：

相似形综合题．

专题：

压轴题．

分析：

（1）当PQ∥BC时，我们可得出三角形APQ和三角形ABC相似，那么可得出关于AP，AB，AQ，AC的比例关系，我们观察这四条线段，已知的有AC，根据P，Q的速度，可以用时间t表示出AQ，BP的长，而AB可以用勾股定理求出，这样也就可以表示出AP，那么将这些数值代入比例关系式中，即可得出t的值．

（2）求三角形APQ的面积就要先确定底边和高的值，底边AQ可以根据Q的速度和时间t表示出来．关键是高，可以用AP和∠A的正弦值来求．AP的长可以用AB﹣BP求得，而sinA就是BC：AB的值，因此表示出AQ和AQ边上的高后，就可以得出y与t的函数关系式．

（3）如果将三角形ABC的周长和面积平分，那么AP+AQ=BP+BC+CQ，那么可以用t表示出CQ，AQ，AP，BP的长，那么可以求出此时t的值，我们可将t的值代入（2）的面积与t的关系式中，求出此时面积是多少，然后看看面积是否是三角形ABC面积的一半，从而判断出是否存在这一时刻．

（4）我们可通过构建相似三角形来求解．过点P作PM⊥AC于M，PN⊥BC于N，那么PNCM就是个矩形，解题思路：通过三角形BPN和三角形ABC相似，得出关于BP，PN，AB，AC的比例关系，即可用t表示出PN的长，也就表示出了MC的长，要想使四边形PQP'C是菱形，PQ=PC，根据等腰三角形三线合一的特点，QM=MC，这样有用t表示出的AQ，QM，MC三条线段和AC的长，就可以根据AC=AQ+QM+MC来求出t的值．求出了t就可以得出QM，CM和PM的长，也就能求出菱形的边长了．

解答：

解：（1）在Rt△ABC中，AB=，

由题意知：AP=5﹣t，AQ=2t，若PQ∥BC，则△APQ∽△ABC，

∴=，∴=，

∴t=．所以当t=时，PQ∥BC．（2）过点P作PH⊥AC于H．

∵△APH∽△ABC，

∴=，

∴=，

∴PH=3﹣t，

∴y=×AQ×PH=×2t×（3﹣t）=﹣t²+3t．（3）若PQ把△ABC周长平分，则AP+AQ=BP+BC+CQ．

∴（5﹣t）+2t=t+3+（4﹣2t），解得t=1．

若PQ把△ABC面积平分，则S_△APQ=S_△ABC，即﹣+3t=3．

∵t=1代入上面方程不成立，

∴不存在这一时刻t，使线段PQ把Rt△ACB的周长和面积同时平分．（4）过点P作PM⊥AC于M，PN⊥BC于N，

若四边形PQP'C是菱形，那么PQ=PC．

∵PM⊥AC于M，

∴QM=CM．

∵PN⊥BC于N，易知△PBN∽△ABC．

∴=，∴=，

∴PN=，

∴QM=CM=，

∴t+t+2t=4，解得：t=．

∴当t=s时，四边形PQP'C是菱形．

此时PM=3﹣t=cm，CM=t=cm，

在Rt△PMC中，PC===cm，

∴菱形PQP′C边长为cm．

点评：

本题图形结合的动态题，是近几年考试热点，同时考查三角形相似知识，是一道很好的综合题．本题亮点是巧妙结合图形综合考查不同知识点．