题目内容
若点P（m，n）在反比例函数
的图象上，则m2n-4m+3的值为________．
3
分析：根据反比例函数图象上点的坐标特征得到mn=4，再把m2n-4m+3变形为m（mn-4）+3，然后利用整体代入的方法进行计算．
解答：∵点P（m，n）在反比例函数的图象上，
∴mn=4，
∴m2n-4m+3=m（mn-4）+3
=m（4-4）+3
=3．
故答案为3．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=
（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
分析：根据反比例函数图象上点的坐标特征得到mn=4，再把m2n-4m+3变形为m（mn-4）+3，然后利用整体代入的方法进行计算．
解答：∵点P（m，n）在反比例函数
的图象上，∴mn=4，
∴m2n-4m+3=m（mn-4）+3
=m（4-4）+3
=3．
故答案为3．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=
（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k． 
练习册系列答案
名校课堂系列答案
相关题目
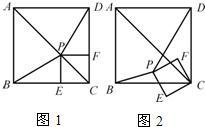25、如图1，已知P为正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．
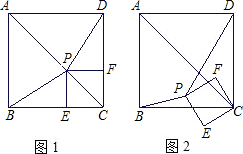的过程中，△PBD的面积是否存在最大值、最小值？如果存在，试求出最大值、最小值；如果不存在，请说明理由．
已知：点O到△ABC的两边AB、AC所在直线的距离相等，且OB=OC，
已知等腰△ABC中，AB=AC，D是BC的中点，将三角板中的90°角的顶点绕D点在△ABC内旋转，角的两边分别与AB、AC交于E、F，且点E、F不与A、B、C三点重合．