题目内容
已知∠AOB=90°，点P在∠AOB的平分线上，OP=6，则点P到OA，OB的距离为
- A.6，6
- B.3，3
- C.3，3
- D.3，3
D
分析：利用角平分线的性质计算．
解答：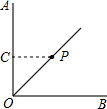
解：作PC⊥OA于C，由题意可得
△OPC是等腰直角三角形，
因为OP=6，
根据勾股定理可得PC=3，
根据角平分线的性质，
点P到OB的距离为3．
故选D．
点评：此题主要考查角平分线的性质和勾股定理．
分析：利用角平分线的性质计算．
解答：
解：作PC⊥OA于C，由题意可得△OPC是等腰直角三角形，
因为OP=6，
根据勾股定理可得PC=3
，根据角平分线的性质，
点P到OB的距离为3
．故选D．
点评：此题主要考查角平分线的性质和勾股定理．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
，1）．
点P不与点O重合．
如图，已知∠AOB=90°，∠AOC=60°，OD平分∠BOC，OE平分∠AOC．
（1）如图，已知∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，求∠MON的度数；