题目内容
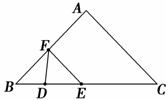
如图,在△ABC中,AB=AC=10 cm,BC=16 ![]() cm,DE=4 cm.动线段DE(端点D从点B开始)沿BC边以1 cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).
cm,DE=4 cm.动线段DE(端点D从点B开始)沿BC边以1 cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).
(1) 直接写出用含t的代数式表示线段BE、EF的长;
(2) 在这个运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,请说明理由;
(3) 设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积.
解 (1) BE=(t+4) cm,EF=![]() (t+4) cm.
(t+4) cm.
(2)分三种情况讨论:



① 当DF=EF时,有∠EDF=∠DEF=∠B,
∴ 点B与点D重合,∴ t=0.
② 当DE=EF时,∴4=![]() (t+4),
(t+4),
解得:t=![]() .
.
③当DE=DF时,
有∠DFE=∠DEF=∠B=∠C,
∴△![]() DEF∽△ABC.∴
DEF∽△ABC.∴![]() =
=![]() ,
,
即![]() =
=![]() ,解得:t=
,解得:t=![]() .
.
综上所述,当t=0、![]() 或
或![]() 秒时,
秒时,
△DEF为等腰三角形.
(3)设P是AC的中点,连接BP,∵EF∥AC,
∴△FBE∽△ABC.∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
又∠BE![]() N=∠C,
N=∠C,
∴△NBE∽△PBC,
∴∠NBE=∠PBC.∴点N沿直线BP运动,MN也随之平移.
如图,设MN从ST位置运动到PQ位置,则四边形PQST是平行四边形.
∵M、N分别是DF、EF的中点,
∴MN∥DE,且ST=MN=![]() DE=2.
DE=2.
分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,
当t=0时,EF=![]() (0+4)=
(0+4)=![]() ,
,
TK=![]() EF·sin∠DEF=
EF·sin∠DEF=![]() ×
×![]() ×
×![]() =
=![]() ;
;
当t=12时,EF=AC=10,
PL=![]() AC·sin C=
AC·sin C=![]() ×10×
×10×![]() =3.
=3.
∴PR=PL-RL=PL-TK=3-![]() =
=![]() .
.
∴S▱PQST=ST·PR=2×![]() =
=![]() .
.
∴整个运动过程中,MN所扫过的面积为![]() cm2.
cm2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=