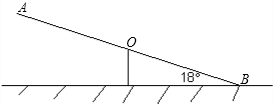
题目内容
如图，跷跷板AB的一端B碰到地面时，AB与地面的夹角为18°，且OA=OB=2m．
（1）求此时另一端A离地面的距离（精确到0.1m）；
（2）跷动AB，使端点A碰到地面，请画出点A运动的路线，并求出点A运动路线长．
（参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）
解：（1）过A作AC⊥BD交BD于点C，
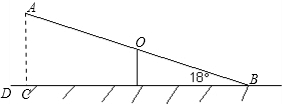
∵AC=ABsin∠ABC=4×0.31≈1.2m．
（2）连接OC，
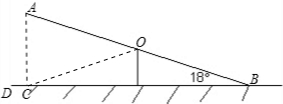
∵O是AB的中点，
∴OC=OA=OB，
∴∠AOC=2∠B=36°，
∴A运动路线长=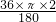
=
．
分析：（1）过A作AC⊥BD较BD与C，根据比例关系及三角函数值可得出AC的值．
（2）根据出OA的长，求出∠AOD的度数，然后利用弧长的计算公式即可得出答案．
点评：本题考查解直角三角形的引用，难度一般，解答本题的关键是正确作出辅助线，然后利用三角函数值求出未知线段的长度．
∵AC=ABsin∠ABC=4×0.31≈1.2m．
（2）连接OC，
∵O是AB的中点，
∴OC=OA=OB，
∴∠AOC=2∠B=36°，
∴A运动路线长=
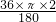=．分析：（1）过A作AC⊥BD较BD与C，根据比例关系及三角函数值可得出AC的值．
（2）根据出OA的长，求出∠AOD的度数，然后利用弧长的计算公式即可得出答案．
点评：本题考查解直角三角形的引用，难度一般，解答本题的关键是正确作出辅助线，然后利用三角函数值求出未知线段的长度．
练习册系列答案
相关题目
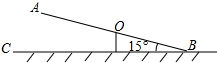（2012•新疆）如图，跷跷板AB的一端B碰到地面时，AB与地面的夹角为15°，且OA=OB=3m．
如图，跷跷板AB的一端B碰到地面时，AB与地面的夹角为15°，且OA=OB=3m．
